设函数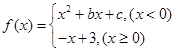.若 (1)求函数的解析式, (2)画出函数的图象.并说出函数的单调区间,(3)若.求相应的值. 题目和参考答案——青夏教育精英家教网—

设函数，若

（1）求函数的解析式；
（2）画出函数的图象，并说出函数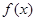的单调区间；
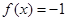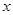（3）若，求相应的值.

（1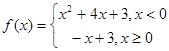）；（2）增区间为，减区间为、；
（3）或x=-2。

解析试题分析：解本小题关键是根据建立b,c的方程，从而解出b,c的值，确定f(x)的解析式，对于分段函数要注意分段求其单调区间.分段画出其图像.
（1），解得

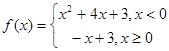------------------------------4
（2）图象略，--------------------------------------------------6
由图象可知单调区间为：
，，,其中增区间为，
减区间为、--------------------------------------8
（3）或x=-2----------------------------------------------------------------------12考点：本小题考查了函数的图像及单调性以及解方程等知识.
点评：分段函数在求解单调区间及最值时，要注意分段求解.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

（本小题满分12分）
已知函数f(x)＝x²＋(2＋lga)x＋lgb，f(－1)＝－2.
(1)求a与b的关系式;
(2)若f(x)≥2x恒成立，求a、b的值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（本题满分13分）
（1）求值: ；
（2）求值: (lg2)²+lg5·lg20+ lg100;
（3）已知. 求a、b，并用表示.

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（本题12分）某公司是专门生产健身产品的企业，第一批产品上市销售40天内全部售完，该公司对第一批产品上市后的市场销售进行调研，结果如图（1）、（2）所示．其中（1）的抛物线表示的是市场的日销售量与上市时间的关系；（2）的折线表示的是每件产品的销售利润与上市时间的关系．

（1）写出市场的日销售量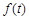与第一批产品A上市时间t的关系式；
（2）第一批产品A上市后的第几天，这家公司日销售利润最大，最大利润是多少？

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（文科题）（本小题12分）
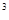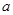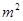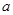要建造一个无盖长方体水池，底面一边长固定为8m，最大装水量为72m，池底和池壁的造价分别为2元／、元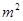／，怎样设计水池底的另一边长和水池的高，才能使水池的总造价最低?最低造价是多少?

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

（本小题满分12分）
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上，在小艇出发时，轮船位于港口的O北偏西30°且与该港口相距20海里的A处，并正以30海里/小时的航行速度沿正东方向匀速行驶. 假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶，经过t小时与轮船相遇.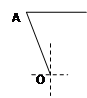

(Ⅰ)若希望相遇时小艇的航行距离最小，则小艇航行时间应为多少小时？
(Ⅱ)为保证小艇在30分钟内（含30分钟）能与轮船相遇，试确定小艇航行速度的最小值；