Question

【题目】设命题p：实数x满足x2﹣4ax+3a2＜0，其中a＞0，命题q：实数x满足 ．
（1）若a=1，且p∧q为真，求实数x的取值范围；
（2）若p是q的充分不必要条件，求实数a的取值范围．

Answer 1

【答案】
（1）解：当a=1时，p：{x|1＜x＜3}，q：{x|2＜x≤3}，又p∧q为真，所以p真且q真，

由 得2＜x＜3，所以实数x的取值范围为（2，3）

（2）解：因为￢p是￢q的充分不必要条件，所以q是p的充分不必要条件，

又p：{x|a＜x＜3a}（a＞0），q：{x|2＜x≤3}，所以 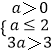解得1＜a≤2，

所以实数a的取值范围是（1，2]

【解析】（1）现将a=1代入命题p，然后解出p和q，又p∧q为真，所以p真且q真，求解实数a的取值范围；（2）先由￢p是￢q的充分不必要条件得到q是p的充分不必要条件，然后化简命题，求解实数a的范围．
【考点精析】利用复合命题的真假对题目进行判断即可得到答案，需要熟知“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反；“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；“p或q”形式复合命题当p与q同为假时为假，其他情况时为真．