
【题目】从8名运动员中选4人参加![]() 米接力赛,在下列条件下,各有多少种不同的排法?
米接力赛,在下列条件下,各有多少种不同的排法?
(1)甲、乙两人必须入选且跑中间两棒;
(2)若甲、乙两人只有一人被选且不能跑中间两棒;
(3)若甲、乙两人都被选且必须跑相邻两棒;
(4)甲不在第一棒.
【答案】(1)60;(2)480;(3)180;(4)1470
【解析】
(1)先![]() 选好参赛选手,再
选好参赛选手,再![]() 安排好甲、乙两人,再
安排好甲、乙两人,再![]() 安排剩余两人,相乘得到结果;(2)先确定参赛选手,共有
安排剩余两人,相乘得到结果;(2)先确定参赛选手,共有![]() 种选法;再
种选法;再![]() 安排好甲或乙,继续
安排好甲或乙,继续![]() 安排好剩余三人,相乘得到结果;(3)先
安排好剩余三人,相乘得到结果;(3)先![]() 选好参赛选手,再用捆绑法求得结果;(4)先
选好参赛选手,再用捆绑法求得结果;(4)先![]() 安排好第一棒,再
安排好第一棒,再![]() 安排好其余三棒,相乘得到结果.
安排好其余三棒,相乘得到结果.
(1)除甲、乙外还需选择![]() 人参加接力赛共有
人参加接力赛共有![]() 种选法
种选法
则甲、乙跑中间两棒共有![]() 种排法;另外
种排法;另外![]() 人跑另外两棒共有
人跑另外两棒共有![]() 种排法
种排法
![]() 甲、乙两人必须入选且跑中间两棒共有:
甲、乙两人必须入选且跑中间两棒共有:![]() 种排法
种排法
(2)甲、乙只有一人入选且选另外选![]() 人参加接力赛共有
人参加接力赛共有![]() 种选法
种选法
甲或乙不跑中间两棒共有![]() 种排法;其余
种排法;其余![]() 人跑剩余三棒共有
人跑剩余三棒共有![]() 种排法
种排法
![]() 甲、乙两人只有一人被选且不能跑中间两棒共有:
甲、乙两人只有一人被选且不能跑中间两棒共有:![]() 种排法
种排法
(3)除甲、乙外还需选择![]() 人参加接力赛共有
人参加接力赛共有![]() 种选法
种选法
甲乙跑相邻两棒,其余![]() 人跑剩余两棒共有
人跑剩余两棒共有![]() 种排法
种排法
![]() 甲、乙两人都被选且必须跑相邻两棒共有:
甲、乙两人都被选且必须跑相邻两棒共有:![]() 种排法
种排法
(4)甲不在第一棒则需选择一人跑第一棒,共有![]() 种选法
种选法
其余三棒共有![]() 种排法
种排法
![]() 甲不在第一棒共有
甲不在第一棒共有![]() 种排法
种排法


科目:高中数学 来源: 题型:
【题目】为了探究某市高中理科生在高考志愿中报考“经济类”专业是否与性别有关,现从该市高三理科生中随机抽取50名学生进行调查,得到如下2×2列联表:(单位:人)

(1)据此样本,判断能否在犯错误的概率不超过0.001的前提下认为理科生报考“经济类”专业与性别有关?
(2)若以样本中各事件的频率作为概率估计全市总体考生的报考情况,现从该市的全体考生(人数众多)中随机抽取3人,设3人中报考“经济类”专业的人数为随机变量X,求随机变量X的概率分布列及数学期望.
附:
![]()
![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.

(1)求出第4组的频率,并补全频率分布直方图;
(2)根据样本频率分布直方图估计样本的中位数与平均数;
(3)如果用分层抽样的方法从“优秀”和“良好”的学生中共选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]()
(3)在(2)条件下,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD中,边长为2,E为AB中点,F是边BC上的动点.
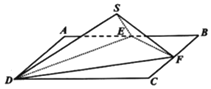
(1)将△ADE沿DE翻折90°到△SDE,求二面角S-DC-E的正切值;
(2)若![]() ,将△ADE沿DE翻折到△SDE,△BEF沿EF翻折到△SEF,接DF,设直线DS与平面DEF所成角为θ,求
,将△ADE沿DE翻折到△SDE,△BEF沿EF翻折到△SEF,接DF,设直线DS与平面DEF所成角为θ,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com