
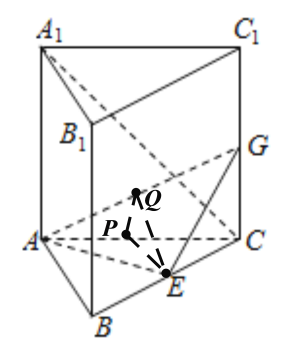
【题目】如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠BAC=90°,AC=AB=AA1,E是BC的中点.

(1)求证:AE⊥B1C;
(2)若G为C1C中点,求二面角C-AG-E的正切值.
【答案】(1)见解析;(2)![]()
【解析】
(1)证明AE⊥BB1和AE⊥BC得到AE⊥面BB1C1C,进而得到证明.
(2)连接AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,证明EP⊥平面ACC1A1得到∠PQE是二面角C-AG-E的平面角,计算得到答案.
(1)因为BB1⊥面ABC,AE面ABC,所以AE⊥BB1
由AB=AC,E为BC的中点得到AE⊥BC·
∵BC∩BB1=B∴AE⊥面BB1C1C
∴AE⊥B1C
(2)如图所示:连接AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,
则EP⊥AC,又∵平面ABC⊥平面ACC1A1
∴EP⊥平面ACC1A1,而PQ⊥AG∴EQ⊥AG.
∴∠PQE是二面角C-AG-E的平面角.
不妨设AB=AC=AA1=2,
则EP=1,AP=1,PQ=![]() ,得tan∠PQE=
,得tan∠PQE=![]() =
=![]()
所以二面角C-AG-E的平面角正切值是![]()


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】关于函数![]()
![]() ,有下列四个命题:①
,有下列四个命题:①![]() 的值域是
的值域是![]() ;②
;②![]() 是奇函数;③
是奇函数;③![]() 在
在![]() 上单调递增;④方程
上单调递增;④方程![]() 总有四个不同的解;其中正确的是( )
总有四个不同的解;其中正确的是( )
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,任取
,任取![]() ,记函数
,记函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() 最小值为
最小值为![]() 记
记![]() . 则关于函数
. 则关于函数![]() 有如下结论:
有如下结论:
①函数![]() 为偶函数;
为偶函数;
②函数![]() 的值域为
的值域为![]() ;
;
③函数![]() 的周期为2;
的周期为2;
④函数![]() 的单调增区间为
的单调增区间为![]() .
.
其中正确的结论有____________.(填上所有正确的结论序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
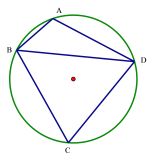
【题目】某城市在进行规划时,准备设计一个圆形的开放式公园.为达到社会和经济效益双丰收.园林公司进行如下设计,安排圆内接四边形![]() 作为绿化区域,其余作为市民活动区域.其中
作为绿化区域,其余作为市民活动区域.其中![]() 区域种植花木后出售,
区域种植花木后出售,![]() 区域种植草皮后出售,已知草皮每平方米售价为
区域种植草皮后出售,已知草皮每平方米售价为![]() 元,花木每平方米的售价是草皮每平方米售价的三倍. 若
元,花木每平方米的售价是草皮每平方米售价的三倍. 若![]() km ,
km ,![]() km
km
(1)若![]() km ,求绿化区域的面积;
km ,求绿化区域的面积;
(2)设![]() ,当
,当![]() 取何值时,园林公司的总销售金额最大.
取何值时,园林公司的总销售金额最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
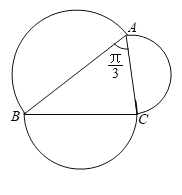
【题目】定义在封闭的平面区域D内任意两点的距离的最大值称为平面区域D的“直径".已知锐角三角形的三个顶点A,B,C在半径为1的圆上,且![]() ,分别以
,分别以![]() 各边为直径向外作三个半圆,这三个半圆和
各边为直径向外作三个半圆,这三个半圆和![]() 构成平面区域D,则平面区域D的“直径”是______.
构成平面区域D,则平面区域D的“直径”是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是由两个全等的菱形
是由两个全等的菱形![]() 和
和![]() 组成的空间图形,
组成的空间图形,![]() ,∠BAF=∠ECD=60°.
,∠BAF=∠ECD=60°.
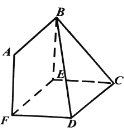
(1)求证:![]() ;
;
(2)如果二面角B-EF-D的平面角为60°,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com