
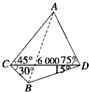
 如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是
如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是| AD |
| sin45° |
| CD |
| sin60° |
| ||||
|
| 6 |
| BD |
| sin30° |
| CD |
| sin135° |
| ||||
|
| 2 |
(3000
|
| 42 |
| 42 |


科目:高中数学 来源: 题型:
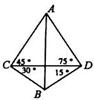 我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知DC=6000米,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图所示).求炮兵阵地到目标的距离(结果保留根号).
我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知DC=6000米,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图所示).求炮兵阵地到目标的距离(结果保留根号).查看答案和解析>>
科目:高中数学 来源:黄冈中学 高一数学(下册)、第五章 平面向量单元(5.6~研究性课题) 题型:044
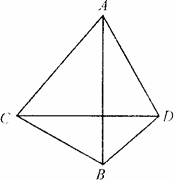
我炮兵阵地位于地面A处,两观察所分别位于地面点C和点D处,已知CD=6000m,∠ACD=45°,∠ADC=75°,目标出现于地面点B处,测得∠BCD=30°,∠BDC=15°(如图所示).求炮兵阵地到目标的距离.
查看答案和解析>>
科目:高中数学 来源:2011年高三数学(文科)一轮复习讲义:3.6 解三角形(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮基础知识训练(30)(解析版) 题型:解答题
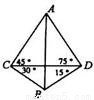
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com