练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    正方体ABCD－A1B1C1D1的棱长为a，求A1C1和平面AB1C间的距离．

    答案：
    解析：

    　　解法1：如图所示，A1C1∥平面AB1C，又平面BB1DD1⊥平面AB1C．

    　　故若过O1作O1E⊥OB1于E，则OE1⊥平面AB1C，O1E为所求的距离

    　　由O1E·OB1＝O1B1·OO1，

    　　可得：O1E＝

    　　解法2：转化为求C1到平面AB1C的距离，也就是求三棱锥C1－AB1C的高h．

    　　由V＝V，可得h＝a．

    　　解法3：因平面AB1C∥平面C1DA1，它们间的距离即为所求，连BD1，分别交B1O、DO1与F、G(图中未画出)．易证BD1垂直于上述两个平面，故FG长即为所求，易求得

    　　FG＝．

    　　点评：(1)求线面距离的先决条件是线面平行，而求线面距离的常用方法是把它们转化为求点面之间的距离，有时也可转化为求面面距离，从本题的解法也可悟出求异面直线之间的距离的思路．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在棱长为1的正方体ABCD-A1B1C1D1中．
    （1）求：点A到平面BD1的距离；
    （2）求点A1到平面AB1D1的距离；
    （3）求平面AB1D1与平面BC1D的距离；
    （4）求直线AB到CDA1B1的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    正方体ABCD-A1B1C1D1的棱长为a．
    求：
    （1）二面角A-BD-A1的正切值；
    （2）AA1与平面A1BD所成的角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2007•河东区一模）已知：正方体ABCD-A1B1C1D1的棱长为1．
    （Ⅰ）求棱AA1与平面A1BD所成的角；
    （Ⅱ）求二面角B-A1D-B1的大小；
    （Ⅲ）求四面体A1-BB1D的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若棱长为1的正方体ABCD-A1B1C1D1 的八个顶点都在球O的表面上，则A，A1两点之间的球面距离为
    		3
    2
    arccos
    1
    3
    		3
    2
    arccos
    1
    3
    ．

    查看答案和解析>>

    科目：高中数学 来源：2013届云南省高二下学期期中考试理科数学试卷（解析版） 题型：选择题

    正方体ABCD－A1 B1 C1 D1中，BB1与平面ACD1所成角的余弦值为    （        ）

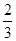     (A)                    (B)             (C)           (D)

     

    查看答案和解析>>

    同步练习册答案