证明:
(1)已知x,y都是正实数,求证:x
3+y
3≥x
2y+xy
2,
(2)已知a,b,c∈R
+,且a+b+c=1,求证:
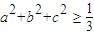
.
【答案】
分析:(1)用比较法证明不等式,(x
3+y
3 )-(x
2y+xy
2)=(x+y)(x-y)
2,分析符号可得结论.
(2)由题意得,1=(a+b+c)
2=a
2+b
2+c
2+2ab+2bc+2ac≤3(a
2+b
2+c
2),结论得证.
解答:证明:(1)∵(x
3+y
3 )-(x
2y+xy
2)=x
2 (x-y)+y
2(y-x)=(x-y)(x
2-y
2 )
=(x+y)(x-y)
2.
∵x,y都是正实数,∴(x-y)
2≥0,(x+y)>0,∴(x+y)(x-y)
2≥0,
∴x
3+y
3≥x
2y+xy
2.
(2)∵a,b,c∈R
+,且a+b+c=1,∴1=(a+b+c)
2=a
2+b
2+c
2+2ab+2bc+2ac
≤3(a
2+b
2+c
2),∴a
2+b
2+c
2≥

,当且仅当a=b=c 时,等号成立.
点评:本题考查用比较法证明不等式,基本不等式的应用,将式子变形是证明的关键.
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
证明:
(1)已知x,y都是正实数,求证:x
3+y
3≥x
2y+xy
2,
(2)已知a,b,c∈R
+,且a+b+c=1,求证:
a2+b2+c2 ≥ .
查看答案和解析>>
科目:高中数学
来源:2011-2012学年宁夏吴忠市盐池高中高三摸底数学试卷(理科)(解析版)
题型:解答题
证明:
(1)已知x,y都是正实数,求证:x
3+y
3≥x
2y+xy
2,
(2)已知a,b,c∈R
+,且a+b+c=1,求证:

.
查看答案和解析>>
科目:高中数学
来源:2012年吉林省实验中学高考数学六模试卷(文科)(解析版)
题型:解答题
证明:
(1)已知x,y都是正实数,求证:x
3+y
3≥x
2y+xy
2,
(2)已知a,b,c∈R
+,且a+b+c=1,求证:

.
查看答案和解析>>
科目:高中数学
来源:2011年辽宁省锦州市高考数学三模试卷(解析版)
题型:解答题
证明:
(1)已知x,y都是正实数,求证:x
3+y
3≥x
2y+xy
2,
(2)已知a,b,c∈R
+,且a+b+c=1,求证:

.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年海南省国兴中学、海师附中、嘉积中学、三亚一中高三联考数学试卷(理科)(解析版)
题型:解答题
证明:
(1)已知x,y都是正实数,求证:x
3+y
3≥x
2y+xy
2,
(2)已知a,b,c∈R
+,且a+b+c=1,求证:

.
查看答案和解析>>

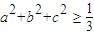 .
. ,当且仅当a=b=c 时,等号成立.
,当且仅当a=b=c 时,等号成立.

 .
. .
. .
. .
.