
已知函数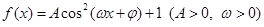 的最大值为3,
的最大值为3,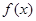 的图像与
的图像与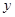 轴的交点坐标为
轴的交点坐标为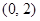 ,其相邻两条对称轴间的距离为
,其相邻两条对称轴间的距离为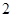 ,则
,则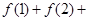
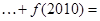 ____________.
____________.
4021或4019
【解析】解:将原函数f(x)=Acos2(ωx+ϕ)+1转化为:f(x)= cos(2ωx+2ϕ)+
cos(2ωx+2ϕ)+ +1
+1
相邻两对称轴间的距离为2可知周期为:4,则2ω= =
= ,ω=
,ω= 最大值为3,可知A=2
最大值为3,可知A=2
又∵图象经过点(0,2),
∴cos2ϕ=0
∴2∅=kπ+
∴f(x)=cos(  x+kπ+
x+kπ+ )+2=2±sin(
)+2=2±sin(  x)
x)
∵f(1)=2+1,f(2)=0+2,f(3)=-1+2,f(4)=0+2…
f(1)+f(2)+f(3)+…+f(2010)=502×8+5=4021
或f(1)=2-1,f(2)=0+2,f(3)=1+2,f(4)=0+2…
f(1)+f(2)+f(3)+…+f(2010)=502×8+3=4019
故答案为:4021或4019


科目:高中数学 来源:2010年广东省高考数学冲刺预测试卷06(理科)(解析版) 题型:解答题
 的最大值为3,f(x)的图象的相邻两对称轴间的距离为2,在y轴上的截距为2.
的最大值为3,f(x)的图象的相邻两对称轴间的距离为2,在y轴上的截距为2.查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷六文科数学 题型:解答题
(本小题满分12分)
已知函数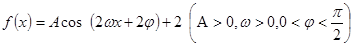 的最大值为3,
的最大值为3,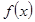 的图像的相邻两对称轴间的距离为2,在y轴上的截距为2.
的图像的相邻两对称轴间的距离为2,在y轴上的截距为2.
(Ⅰ)求函数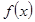 的解析式;
的解析式;
(Ⅱ)若m=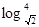 ,求f(m)+f(m+1)的值.
,求f(m)+f(m+1)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com