
【题目】为了解本届高二学生对文理科的选择与性别是否有关,现随机从高二的全体学生中抽取了若干名学生,据统计,男生35人,理科生40人,理科男生30人,文科女生15人。
(1)完成如下2×2列联表,判断是否有99.9%的把握认为本届高二学生“对文理科的选择与性别有关”?
男生 | 女生 | 合计 | |
文科 | |||
理科 | |||
合计 |
(2)已采用分层抽样的方式从样本的所有女生中抽取了5人,现从这5人中随机抽取2人参加座谈会,求抽到的2人恰好一文一理的概率。
| 0.15 | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式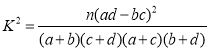 ,其中
,其中![]() 为样本容量)
为样本容量)
科目:高中数学 来源: 题型:
【题目】某地区某长产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若近几年该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的函数关系式为
满足的函数关系式为![]() ,且每年该农产品都能售完.
,且每年该农产品都能售完.
①根据(1)中所建立的回归方程预测该地区2018(![]() )年该农产品的产量;
)年该农产品的产量;
②当![]() (
(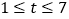 )为何值时,销售额
)为何值时,销售额![]() 最大?
最大?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: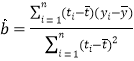 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秸秆还田是当今世界上普通重视的一项培肥地力的增产措施,在杜绝了秸秆焚烧所造成的大气污染的同时还有增肥增产作用.某农机户为了达到在收割的同时让秸秆还田,花![]() 元购买了一台新型联合收割机,每年用于收割可以收入
元购买了一台新型联合收割机,每年用于收割可以收入![]() 万元(已减去所用柴油费);该收割机每年都要定期进行维修保养,第一年由厂方免费维修保养,第二年及以后由该农机户付费维修保养,所付费用
万元(已减去所用柴油费);该收割机每年都要定期进行维修保养,第一年由厂方免费维修保养,第二年及以后由该农机户付费维修保养,所付费用![]() (元)与使用年数
(元)与使用年数![]() 的关系为:
的关系为:![]() ,已知第二年付费
,已知第二年付费![]() 元,第五年付费
元,第五年付费![]() 元.
元.
(1)试求出该农机户用于维修保养的费用![]() (元)与使用年数
(元)与使用年数![]() 的函数关系;
的函数关系;
(2)这台收割机使用多少年,可使平均收益最大?(收益=收入-维修保养费用-购买机械费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从集合![]() 的所有非空子集中,等可能地取出
的所有非空子集中,等可能地取出![]() 个.
个.
(1)若![]() ,求所取子集的元素既有奇数又有偶数的概率;
,求所取子集的元素既有奇数又有偶数的概率;
(2)若![]() ,记所取子集的元素个数之差为
,记所取子集的元素个数之差为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: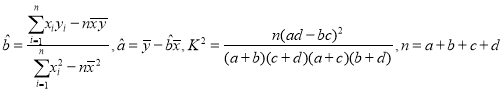 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上的最大值为2.
上的最大值为2.
(1)求函数![]() 的解析式,并求它的对称中心的坐标;
的解析式,并求它的对称中心的坐标;
(2)先将函数![]() 保持横坐标不变,纵坐标变为原来的
保持横坐标不变,纵坐标变为原来的![]() (
(![]() )倍,再将图象向左平移
)倍,再将图象向左平移![]() (
(![]() )个单位,得到的函数
)个单位,得到的函数![]() 为偶函数.若对任意的
为偶函数.若对任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的方程为![]() x﹣3y+3=0.
x﹣3y+3=0.
(Ⅰ)若直线l1与l在y轴上的截距相等,且l1的倾斜角是l的倾斜角的两倍,求直线l1的一般式方程;
(Ⅱ)若直线l2过点(![]() ,2),且l2与l垂直求直线l2的斜截式方程.
,2),且l2与l垂直求直线l2的斜截式方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国庆![]() 周年庆典活动中,东城区教育系统近
周年庆典活动中,东城区教育系统近![]() 名师生参与了国庆中心区合唱、
名师生参与了国庆中心区合唱、![]() 方阵群众游行、联欢晚会及
方阵群众游行、联欢晚会及![]() 万只气球保障等多项重点任务.设
万只气球保障等多项重点任务.设![]() 是参与国庆中心区合唱的学校
是参与国庆中心区合唱的学校![]() ,
,![]() 是参与27方阵群众游行的学校
是参与27方阵群众游行的学校![]() ,
,![]() 是参与国庆联欢晚会的学校
是参与国庆联欢晚会的学校![]() .请用上述集合之间的运算来表示:①既参与国庆中心区合唱又参与27方阵群众游行的学校的集合为_____;②至少参与国庆中心区合唱与国庆联欢晚会中一项的学校的集合为_____.
.请用上述集合之间的运算来表示:①既参与国庆中心区合唱又参与27方阵群众游行的学校的集合为_____;②至少参与国庆中心区合唱与国庆联欢晚会中一项的学校的集合为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).

(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com