
分析 由2an+2an+2+5Sn=5Sn+1,可得2an+2an+2=5an+1,2+2q2=5q,且a1=q>1,解得a1=q=2.可得bn=2n•|sin$\frac{(n+1)π}{2}$|,对n分类讨论即可得出.
解答 解:由2an+2an+2+5Sn=5Sn+1,∴2an+2an+2=5an+1,∴2+2q2=5q,且a1=q>1,
解得a1=q=2.
∴an=2n.
∵数列{bn}满足$\frac{{b}_{n}}{{a}_{n}}$=|sin$\frac{(n+1)π}{2}$|.∴bn=2n•|sin$\frac{(n+1)π}{2}$|,
∴b2n-1=22n-1•|sin(nπ)|=0,b2n=22n$|sin\frac{(2n+1)π}{2}|$=22n.
∵数列{bn}的前m项和为340,假设m=2n.
∴b2+b4+…+b2n=22+24+…+22n=340,
∴$\frac{4({4}^{n}-1)}{4-1}$=340,解得n=4.
∴m=8.
∵a9=0.
∴m=9时也满足条件.
∴m=8或9.
故答案为:8或9.
点评 本题考查了等比数列的通项公式与求和公式、分类讨论方法、分组求和方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-2,4) | B. | (-1,3] | C. | [-2,-1] | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
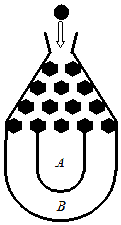 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落的过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
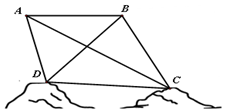 为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.
为绘制海底地貌图,测量海底两点C,D间的距离,海底探测仪沿水平方向在A,B两点进行测量,A,B,C,D在同一个铅垂平面内.海底探测仪测得∠BAC=30°,∠DAC=45°,∠ABD=45°,∠DBC=75°,同时测得$AB=\sqrt{3}$海里.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2e-3}{2e}$ | B. | $\frac{3}{2e}$ | C. | $\frac{{e}^{e}{-e}^{2}+e-1}{e}$ | D. | $\frac{e-1}{e+1}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com