
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).
(1)若![]() ,
, ![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() ,且
,且![]() ,求函数
,求函数![]() 在
在![]() 上的最小值及相应的
上的最小值及相应的![]() 值;
值;
(3)设![]() ,若存在
,若存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(Ⅱ)当
;(Ⅱ)当![]() ,
, ![]() 时,最小值为1;当
时,最小值为1;当![]() ,
, ![]() 时,最小值为
时,最小值为![]() ; (Ⅲ)
; (Ⅲ)![]() .
.
【解析】试题分析:(Ⅰ)代入![]() 的值,求得
的值,求得![]() ,然后由
,然后由![]() 的符号得到单调区间;(Ⅱ)分
的符号得到单调区间;(Ⅱ)分![]() 与
与![]() 两种情况讨论
两种情况讨论![]() 的单调性,求出各段的最小值;(Ⅲ)根据题意将问题转化为
的单调性,求出各段的最小值;(Ⅲ)根据题意将问题转化为![]() ,设
,设![]() ,然后通过求导讨论函数
,然后通过求导讨论函数![]() 的单调性求得实数
的单调性求得实数![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ) ![]() 时,
时, ![]() ,
,
定义域为![]() ,
, ![]()
在![]() 上,
上, ![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]()
所以,函数![]() 的单调增区间为
的单调增区间为![]() ;单调减区间为
;单调减区间为![]()
(Ⅱ)因为![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() ,
, ![]()
(Ⅰ)若![]() ,
,![]() 在
在![]() 上非负(仅当
上非负(仅当![]() 时,
时, ![]() ),
),
故函数![]() 在
在![]() 上是增函数,此时
上是增函数,此时![]()
(Ⅱ)若![]() ,
, 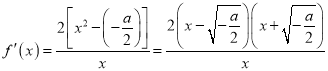 ,
, ![]()
当![]() 时,
时, ![]() ,
, ![]()
当![]() 时,
时, ![]() ,此时
,此时![]() 是减函数;
是减函数;
当![]() 时,
时, ![]() ,此时
,此时![]() 是增函数,
是增函数,
故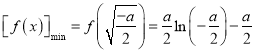
(Ⅲ)![]() ,
, ![]()
不等式![]() ,即
,即![]() 可化为
可化为![]() .
.
因为![]() , 所以
, 所以![]() 且等号不能同时取,
且等号不能同时取,
所以![]() ,即
,即![]() ,因而
,因而![]() (
(![]() )
)
令![]() (
(![]() ),又
),又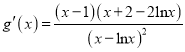 ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
,
从而![]() (仅当
(仅当![]() 时取等号),所以
时取等号),所以![]() 在
在![]() 上为增函数,
上为增函数,
故![]() 的最小值为
的最小值为![]() ,所以实数
,所以实数![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】某地高中年级学生某次身体素质体能测试的原始成绩采用百分制,已知这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表,并规定:
内,发布成绩使用等级制,各等级划分标准见下表,并规定: ![]() 三级为合格,
三级为合格, ![]() 级为不合格
级为不合格
 为了了解该地高中年级学生身体素质情况,从中抽取了
为了了解该地高中年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 分组作出频率分布直方图如图
分组作出频率分布直方图如图![]() 所示,样本中分数在
所示,样本中分数在![]() 分及以上的所有数据的茎叶图如图
分及以上的所有数据的茎叶图如图![]() 所示.
所示.
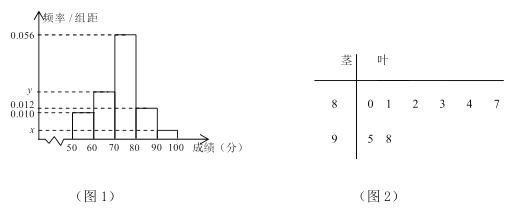
(Ⅰ) 求![]() 及频率分布直方图中
及频率分布直方图中![]() 的值;
的值;
(Ⅱ) 根据统计思想方法,以事件发生的频率作为相应事件发生的概率,若在该地高中学生中任选![]() 人,求至少有
人,求至少有![]() 人成绩是合格等级的概率;
人成绩是合格等级的概率;
(Ⅲ)上述容量为![]() 的样本中,从
的样本中,从![]() 两个等级的学生中随机抽取了
两个等级的学生中随机抽取了![]() 名学生进行调研,记
名学生进行调研,记![]() 为所抽取的
为所抽取的![]() 名学生中成绩为
名学生中成绩为![]() 等级的人数,求随机变量
等级的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(A)在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为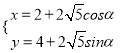 (
(![]() 为参数),
为参数), ![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 为线段
为线段![]() 的中点,设点
的中点,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的坐标方程;
的坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 异于极点的交点为
异于极点的交点为![]() ,与曲线
,与曲线![]() 异于极点的交点为
异于极点的交点为![]() ,求
,求![]() .
.
(B)设函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)对任意![]() ,
, ![]() 不等式
不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点![]() ,焦点在
,焦点在![]() 轴上的椭圆,离心率
轴上的椭圆,离心率![]() ,且椭圆过点
,且椭圆过点![]() .
.
(1)求椭圆的方程;
(2)设椭圆左、右焦点分别为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某生产线上质量监督员甲对产品质量好坏有无影响,现统计数据如下:质量监督员甲在生产现场时,990件产品中合格品有982件,次品有8件;甲不在生产现场时,510件产品中合格品有493件,次品有17件,试分别用列联表、独立性检验的方法分析监督员甲是否在生产现场对产品质量好坏有无影响?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产![]() 和
和![]() 两种产品,按计划每天生产
两种产品,按计划每天生产![]() 各不得少于10吨,已知生产
各不得少于10吨,已知生产![]() 产品
产品![]() 吨需要用煤9吨,电4度,劳动力3个(按工作日计算).生产
吨需要用煤9吨,电4度,劳动力3个(按工作日计算).生产![]() 产品1吨需要用煤4吨,电5度,劳动力10个,如果
产品1吨需要用煤4吨,电5度,劳动力10个,如果![]() 产品每吨价值7万元,
产品每吨价值7万元, ![]() 产品每吨价值12万元,而且每天用煤不超过300吨,用电不超过200度,劳动力最多只有300个,每天应安排生产
产品每吨价值12万元,而且每天用煤不超过300吨,用电不超过200度,劳动力最多只有300个,每天应安排生产![]() 两种产品各多少才是合理的?
两种产品各多少才是合理的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com