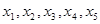练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知一组数据的平均数是2，方差是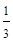，那么另一组数据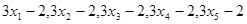的平均数和方差分别为（ ）
    A．2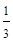，B．4，3C．4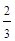，D．2，1
    B
    ∵当一组数据中的每一个数据发生什么样的变化其平均数就发生什么样的变化，
    ∴3x1-2，3x2-2，3x3-2，3x4-2，3x5-2的平均数数据x1，x2，x3，x4，x5的平均数的3倍减2，
    ∵数据x1，x2，x3，x4，x5的平均数是2，
    ∴3x1-2，3x2-2，3x3-2，3x4-2，3x5-2的平均数为：3×2-2=4，
    ∵当一组数据同时加上一个常数不影响方差，以一个常数则其方差变为原来的常数的平方倍，
    ∴3x1-2，3x2-2，3x3-2，3x4-2，3x5-2的方差为：32×=3．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    某重点中学的高二英语老师Vivien，为调查学生的单词记忆时间开展问卷调查。发现在回收上来的1000份有效问卷中，有600名同学们背英语单词的时间安排在白天，另外400名学生晚上临睡前背。Vivien老师用分层抽样的方法抽取50名学生进行实验，实验方法是使两组学生记忆40个无意义音节（如XIQ、GEH），均要求在刚能全部记清时就停止识记，并在8小时后进行记忆测验。不同的是，甲组同学识记结束后一直不睡觉，8小时后测验；乙组同学识记停止后立刻睡觉，8小时后叫醒测验。
    乙组同学识记停止8小时后的准确回忆（保持）情况如图。

    （1）由分层抽样方法，抽取的50名学生乙组应有几名？
    （2）从乙组准确回忆音节数在[8,20)范围内的学生中随机选2人，求两人均准确回忆12个（含12个）以上的概率；
    （3）若从是否睡前记忆单词和单词小测能否优秀进行统计，运用22列联表进行独立性检验，经计算K2=4．069，参考下表你能得到什么统计学结论？
    P(K≥k0)
    		0.100
    		0.050
    		0.025
    		0.010
    		0.001

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    在某项才艺竞赛中，有9位评委，主办单位规定计算参赛者比赛成绩的规则如下：剔除评委中的一个最高分和一个最低分，再计算其他7位评委的平均分作为此参赛者的比赛成绩，现有一位参赛者所获9位评委一个最高分为86分，一个最低分为45分，若未剔除最高分与最低分时9位评委的平均分为76分，则这位参赛者的比赛成绩为______分。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    经统计，某小店卖出的饮料杯数y杯与当天气温x℃的回归方程为．若天气预报说“明天气温为2℃”，则该小店明天大约可卖出饮料  杯．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某样本数据的频率分布直方图的部分图形如右图所示，则数据在[50,70)的频率约为(  　)
    A．0.25B．0.05C．0.5 D．0.025

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    10个小球分别编号为1,2,3,4，其中1号球4个，2号球2个，3号球3个，4号球1个，数0.4是指1号球占总体分布的（   ）
    A．频数B．频率C．D．累积频率

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    下表是某地区的一种传染病与饮用水的调查表:
     
    		得病
    		不得病
    		合计
    干净水
    		52
    		466
    		518
    不干净水
    		94
    		218
    		312
    合计
    		146
    		684
    		830
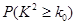    利用列联表的独立性检验,判断能否以99.9%的把握认为“该地区的传染病与饮用不干净的水有关”
    参考数据：
     
    		0．25
    		0．15
    		0．10
    		0．05
    		0．025
    		0．010
    		0．005
    		0．001

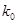    		1．323
    		2．072
    		2．706
    		3．841
    		5．024
    		6．635
    		7．879
    		10．828

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    为适应新课改，切实减轻学生负担，提高学生综合素质，某市某学校高三年级文科生300人在数学选修4-4、4-5、4-7选课方面进行改革，由学生自由选择2门（不可多选或少选），选课情况如下表：
     
    		4-4
    		4-5
    		4-7
    男生
    		130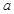

    		80
    女生

    		100
    		60
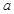    （1）为了解学生情况，现采用分层抽样方法抽取了三科作业共50本，统计发现4-5有18本，试根据这一数据求出，的值.
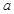    （2）为方便开课，学校要求≥110，＞110，计算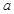＞的概率.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
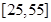    某班同学利用国庆节进行社会实践，对岁的人群随机抽取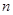人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：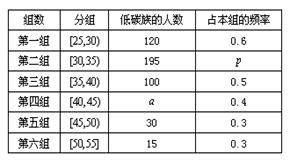

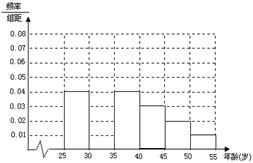
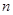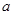    （Ⅰ）补全频率分布直方图并求、、的值；
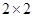    （Ⅱ）为调查该地区的年龄与生活习惯是否符合低碳观念有无关系，调查组按40岁以下为青年，40岁以上(含40岁)为老年分成两组，请你先完成下列维列表，并判断能否有99.9％的把握认定该地区的生活习惯是否符合低碳观念与人的年龄有关？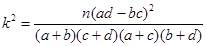
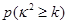    参考公式：

    		0.050
    		      0.010
    		       0.001
             k
    		       3.841
    		      6.635
    		      10.828
    是否低碳族                           年龄组
    		青年
    		老年
    低碳族
    		   
    		   
    非低碳族
    		   
    		   
     

    查看答案和解析>>

    同步练习册答案