
某工厂生产 、
、 两种元件,其质量按测试指标划分为:大于或等于
两种元件,其质量按测试指标划分为:大于或等于 为正品,小于
为正品,小于 为次品.现从一批产品中随机抽取这两种元件各
为次品.现从一批产品中随机抽取这两种元件各 件进行检测,检测结果记录如下:
件进行检测,检测结果记录如下:
 |  |  |  |  |  |
| B |  |  |  |  |  |
 、
、 看不清,统计员只记得
看不清,统计员只记得 ,且
,且 、
、 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等. 与
与 的值;
的值; 件
件 种元件中任取
种元件中任取 件,求
件,求 件都为正品的概率.
件都为正品的概率. (1) ,
, ;(2)
;(2) .
.
解析试题分析:(1)根据 、
、 两种元件的检测数据的平均数与方差分别相等,利用平均数与方差的计算公式列方程组求出
两种元件的检测数据的平均数与方差分别相等,利用平均数与方差的计算公式列方程组求出 与
与 的值;(2)将
的值;(2)将 件
件 元件编号,并将说明哪些是正品,利用列举法将所有的基本事件与问题中涉及事件所包含的基本进行列举,然后利用古典概型的概率计算公式求出相应事件的概率.
元件编号,并将说明哪些是正品,利用列举法将所有的基本事件与问题中涉及事件所包含的基本进行列举,然后利用古典概型的概率计算公式求出相应事件的概率.
试题解析:(1)因为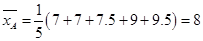 ,
, ,
,
由 ,得
,得 ,①
,①
因为 ,
, ,
,
由 ,得
,得 ,②
,②
由①②解得 或
或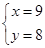 ,
,
因为 ,所以
,所以 ,
, ;
;
(2)记被检测的 件的
件的 种元件分别为
种元件分别为 、
、 、
、 、
、 、
、 ,其中
,其中 、
、 、
、 、
、 为正品,
为正品,
从中任取 件,共有
件,共有 个基本事件,列举如下:
个基本事件,列举如下: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 ,
,
记“ 件都为正品”为事件
件都为正品”为事件 ,则事件
,则事件 包含以下
包含以下 个基本事件:
个基本事件: 、
、 、
、 、
、 、
、 、
、 ,
, ,所以
,所以 件都为正品的概率为
件都为正品的概率为 .
.
考点:1.平均数与方差;2.古典概型


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测.检测的数据如下:
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3) 现从A班的上述5名学生中随机选取3名学生,用X表示其中视力大于4.6的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于 小于
小于 为二等品,小于
为二等品,小于 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
| 测试指标 |  |  |  |  |  |  |
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.
(1)根据图中的数据信息,写出众数 ;
;
(2)小明的父亲上班离家的时间 在上午
在上午 之间,而送报人每天在
之间,而送报人每天在 时刻前后
时刻前后
半小时内把报纸送达(每个时间点送达的可能性相等).
①求小明的父亲在上班离家前能收到报纸(称为事件 )的概率;
)的概率;
②求小明的父亲周一至周五在上班离家前能收到报纸的天数 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在电阻碳含量对于电阻的效应研究中,得到如下表所示的数据:
| 含碳量 (x/%) | 0.10 | 0.30 | 0.40 | 0.55 | 0.70 | 0.80 | 0.95 |
| 20 ℃时电阻 (y/Ω) | 15 | 18 | 19 | 21 | 22.6 | 23.8 | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有甲、乙两个工厂生产同一种产品,产品分为一等品和二等品.为了考察这两个工厂的产品质量的水平是否一致,从甲、乙两个工厂中分别随机地抽出产品109件,191件,其中甲工厂一等品58件,二等品51件,乙工厂一等品70件,二等品121件.
(1)根据以上数据,建立2×2列联表;
(2)试分析甲、乙两个工厂的产品质量有无显著差别(可靠性不低于99%).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,-1代表“生活不能自理”。
(1)随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是多少?
(2)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一汽车厂生产 、
、 、
、 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆)
| | 轿车 | 轿车 | 轿车 |
| 舒适型 |  |  |  |
| 标准型 |  |  |  |
 辆,其中有
辆,其中有 类轿车
类轿车 辆.
辆. 的值;
的值; 类轿车中抽取一个容量为
类轿车中抽取一个容量为 的样本.将该样本看成一个总体,从中任取
的样本.将该样本看成一个总体,从中任取 辆,求至少有
辆,求至少有 辆舒适型轿车的概率;
辆舒适型轿车的概率; 类舒适型轿车中抽取
类舒适型轿车中抽取 辆,经检测它们的得分如下:
辆,经检测它们的得分如下: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 .把这
.把这 辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值
辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.
(1)求图中实数a的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com