
| A. | 如果直线m∥平面α,直线n?α内,那么m∥n | |
| B. | 如果平面α⊥平面β,任取直线m?α,那么必有m丄β | |
| C. | 若直线m∥平面α,直线n∥平面α,则m∥n | |
| D. | 如果平面a外的一条直线m垂直于平面a内的两条相交直线,那么m⊥α |
分析 在A中,m与n平行或异面;在B中,m与β相交、平行或m?β;在C中,m与n相交、平行或异面;在D中,由线面垂直的判定定理得m⊥α.
解答 解:在A中,如果直线m∥平面α,直线n?α内,那么m与n平行或异面,故A错误;
在B中,如果平面α⊥平面β,任取直线m?α,那么m与β相交、平行或m?β,故B错误;
在C中,若直线m∥平面α,直线n∥平面α,则m与n相交、平行或异面,故C错误;
在D中,如果平面a外的一条直线m垂直于平面a内的两条相交直线,
那么由线面垂直的判定定理得m⊥α,故D正确.
故选:D.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | M∩N={(-1,1)} | B. | M∩N=∅ | C. | M⊆N | D. | N⊆M |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{7\sqrt{2}}}{10}$ | C. | $\frac{{\sqrt{2}}}{10}$ | D. | $-\frac{{\sqrt{2}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
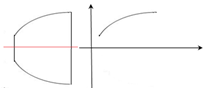 学完解析几何和立体几何后,某同学发现自己家碗的侧面可以看做抛物线的一部分曲线围绕其对称轴旋转而成,他很想知道抛物线的方程,决定把抛物线的顶点确定为原点,对称轴确定为x轴,建立如图所示的平面直角坐标系,但是他无法确定碗底中心到原点的距离,请你通过对碗的相关数据的测量以及进一步的计算,帮助他求出抛物线的方程.你需要测量的数据是碗底的直径2m,碗口的直径2n,碗的高度h(所有测量数据用小写英文字母表示),算出的抛物线标准方程为y2=$\frac{{n}^{2}-{m}^{2}}{h}$x.
学完解析几何和立体几何后,某同学发现自己家碗的侧面可以看做抛物线的一部分曲线围绕其对称轴旋转而成,他很想知道抛物线的方程,决定把抛物线的顶点确定为原点,对称轴确定为x轴,建立如图所示的平面直角坐标系,但是他无法确定碗底中心到原点的距离,请你通过对碗的相关数据的测量以及进一步的计算,帮助他求出抛物线的方程.你需要测量的数据是碗底的直径2m,碗口的直径2n,碗的高度h(所有测量数据用小写英文字母表示),算出的抛物线标准方程为y2=$\frac{{n}^{2}-{m}^{2}}{h}$x.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
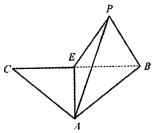 等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P-AE-C为120°,设点P在面ABE上的射影为H.
等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P-AE-C为120°,设点P在面ABE上的射影为H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com