
【题目】平行四边形ABCD中,∠A![]() ,2AB=BC,E,F分别是BC,AD的中点.将四边形DCEF沿着EF折起,使得平面ABEF⊥平面DCEF,得到三棱柱AFD﹣BEC.
,2AB=BC,E,F分别是BC,AD的中点.将四边形DCEF沿着EF折起,使得平面ABEF⊥平面DCEF,得到三棱柱AFD﹣BEC.
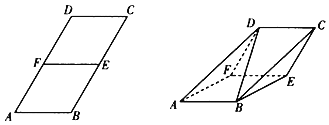
(1)证明:DB⊥EF;
(2)若AB=2,求三棱柱AFD﹣BEC的体积.
【答案】(1)证明见解析;(2)3
【解析】
(1)取EF的中点O,连接OD,OB,ED,FB,可得△BEF,△DEF是等边三角形.可得OD⊥EF,OB⊥EF,由直线与平面垂直的判定可得EF⊥平面BOD,进一步得到DB⊥EF;
(2)三棱柱AFD﹣BEC可分为四棱锥D﹣ABEF与三棱锥B﹣CDE.由(1)知OD⊥EF,结合面面垂直的性质可得OD⊥平面ABEF,同理可证OB⊥平面DCEF,分别求出两个棱锥的体积,作和得答案.
(1)证明:取EF的中点O,连接OD,OB,ED,FB,
可得△BEF,△DEF是等边三角形.
∴OD⊥EF,OB⊥EF,
∵OD∩OB=O,∴EF⊥平面BOD,
而BD平面BOD,
∴DB⊥EF;
(2)解:三棱柱AFD﹣BEC可分为四棱锥D﹣ABEF与三棱锥B﹣CDE.
由(1)知OD⊥EF,而平面ABEF⊥平面DCEF,且交线为EF,
∴OD⊥平面ABEF.
同理可证OB⊥平面DCEF.
四棱锥D﹣ABEF的体积![]() ,
,
三棱锥B﹣CDE的体积![]() ,
,
∴三棱柱AFD﹣BEC的体积V=2+1=3.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,已知a1+a3=12,a2+a4=18,n∈N*.
(1)求数列{an}的通项公式;
(2)求a3+a6+a9+…+a3n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月底因新型冠状病毒感染的肺炎疫情形势严峻,避免外出是减少相互交叉感染最有效的方式.在家中适当锻炼,合理休息,能够提高自身免疫力,抵抗该种病毒.某小区为了调查“宅”家居民的运动情况,从该小区随机抽取了100位成年人,记录了他们某天的锻炼时间,其频率分布直方图如下:
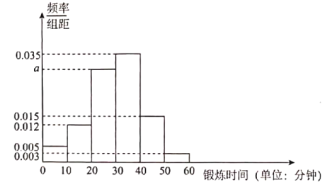
(1)求a的值,并估计这100位居民锻炼时间的平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)小张是该小区的一位居民,他记录了自己“宅”家7天的锻炼时长:
序号n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
锻炼时长m(单位:分钟) | 10 | 15 | 12 | 20 | 30 | 25 | 35 |
(Ⅰ)根据数据求m关于n的线性回归方程;
(Ⅱ)若![]() (
(![]() 是(1)中的平均值),则当天被称为“有效运动日”.估计小张“宅”家第8天是否是“有效运动日”?
是(1)中的平均值),则当天被称为“有效运动日”.估计小张“宅”家第8天是否是“有效运动日”?
附;在线性回归方程![]() 中,
中,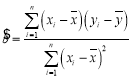 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 长轴长为4,右焦点
长轴长为4,右焦点![]() 到左顶点的距离为3.
到左顶点的距离为3.
(1)求椭圆![]() 的方程;
的方程;
(2)设过原点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点(
两点(![]() 不在坐标轴上),连接
不在坐标轴上),连接![]() 并延长交椭圆于点
并延长交椭圆于点![]() ,若
,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
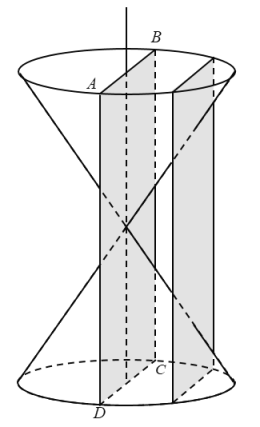
【题目】古希腊数学家阿波罗尼奥斯在他的著作《圆锥曲线论》中记载了用平面切制圆锥得到圆锥曲线的方法.如图,将两个完全相同的圆锥对顶放置(两圆锥的轴重合),已知两个圆锥的底面半径为1,母线长均为![]() ,记过圆锥轴的平面ABCD为平面
,记过圆锥轴的平面ABCD为平面![]() (
(![]() 与两个圆锥面的交线为AC、BD),用平行于
与两个圆锥面的交线为AC、BD),用平行于![]() 的平面截圆锥,该平面与两个圆锥侧面的截线即为双曲线E的一部分,且双曲线E的两条渐近线分别平行于AC、BD,则双曲线E的离心率为( )
的平面截圆锥,该平面与两个圆锥侧面的截线即为双曲线E的一部分,且双曲线E的两条渐近线分别平行于AC、BD,则双曲线E的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com