
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若对任意的
时,若对任意的![]() ,总存在
,总存在![]() 使
使![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 的值域为区间
的值域为区间![]() ,是否存在常数
,是否存在常数![]() ,使区间
,使区间![]() 的长度为
的长度为![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由.(柱:区间
的值,若不存在,请说明理由.(柱:区间![]() 的长度为
的长度为![]() )
)
【答案】(1)![]()
![]() ;(2)
;(2)![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】试题分析:![]() 求出函数的对称轴,得到函数的单调性,解关于
求出函数的对称轴,得到函数的单调性,解关于![]() 的不等式组,解出即可;
的不等式组,解出即可;
![]() 只需函数
只需函数![]() 的值域是函数
的值域是函数![]() 的值域的子集,通过讨论
的值域的子集,通过讨论![]() ,
,![]() ,
,![]() 的情况,得到函数的单调性,从而确定
的情况,得到函数的单调性,从而确定![]() 的范围即可;
的范围即可;
![]() 通过讨论
通过讨论![]() 的范围,结合函数的单调性以及
的范围,结合函数的单调性以及![]() ,
,![]() 的值,得到关于
的值,得到关于![]() 的方程,解出即可。
的方程,解出即可。
解析:(1)根据题意得:![]() 的对称轴是
的对称轴是![]() ,故
,故![]() 在区间
在区间![]() 递增,
递增,
因为函数在区间![]() 上存在零点,故有
上存在零点,故有![]() ,即
,即![]() ,
,
故所求实数![]() 的范围是
的范围是![]() ;
;
(2)若对任意的![]() ,总存在
,总存在![]() ,使
,使![]() 成立,
成立,
只需函数![]() 的值域是函数
的值域是函数![]() 的值域的子集,
的值域的子集,
![]() 时,
时,![]() 的值域是
的值域是![]() ,
,
下面求![]() ,
,![]() 的值域,
的值域,
令![]() ,则
,则![]() ,
,![]() ,
,
①![]() 时,
时,![]() 是常数,不合题意,舍去;
是常数,不合题意,舍去;
②![]() 时,
时,![]() 的值域是
的值域是![]() ,
,
要使![]()
![]() ,只需
,只需![]() ,计算得出
,计算得出![]() ;
;
③![]() 时,
时,![]() 的值域是
的值域是![]() ,
,
要使![]()
![]() ,只需
,只需![]() ,计算得出
,计算得出![]() ;
;
综上,![]() 的范围是
的范围是![]() .
.
(3)根据题意得![]() ,计算得出
,计算得出![]() ,
,
①![]() 时,在区间
时,在区间![]() 上,
上,![]() 最大,
最大,![]() 最小,
最小,
![]() ,
,
计算得出:![]() 或
或![]() (舍去);
(舍去);
②![]() 时,在区间
时,在区间![]() 上,
上,![]() 最大,
最大,![]() 最小,
最小,
![]() ,计算得出:
,计算得出:![]() ;
;
③![]() 时,在区间
时,在区间![]() 上,
上,![]() 最大,
最大,![]() 最小,
最小,
![]() ,
,
计算得出:![]() 或
或![]() ,故此时不存在常数
,故此时不存在常数![]() 满足题意,
满足题意,
综上,存在常数![]() 满足题意,
满足题意,![]() 或
或![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】以下四个命题: ①已知随机变量X~N(0,σ2),若P(|X|<2)=a,则P(X>2)的值为 ![]() ;
;
②设a、b∈R,则“log2a>log2b”是“2a﹣b>1”的充分不必要条件;
③函数f(x)= ![]() ﹣(
﹣( ![]() )x的零点个数为1;
)x的零点个数为1;
④命题p:n∈N,3n≥n2+1,则¬p为n∈N,3n≤n2+1.
其中真命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, ![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 时从区间
时从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=cosx的图象与直线x= ![]() ,x=
,x= ![]() 以及x轴所围成的图形的面积为a,则(x﹣
以及x轴所围成的图形的面积为a,则(x﹣ ![]() )(2x﹣
)(2x﹣ ![]() )5的展开式中的常数项为(用数字作答).
)5的展开式中的常数项为(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形SABC中,∠B=∠C= ![]() ,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB.
,D为边SC上的点,且AD⊥SC,现将△SAD沿AD折起到达PAD的位置(折起后点S记为P),并使得PA⊥AB. 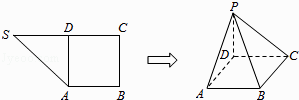
(1)求证:PD⊥平面ABCD;
(2)已知PD=AD,PD+AD+DC=6,G是AD的中点,当线段PB取得最小值时,则在平面PBC上是否存在点F,使得FG⊥平面PBC?若存在,确定点F的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知MOD函数是一个求余函数,记MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2.如图是某个算法的程序框图,若输入m的值为48时,则输出i的值为( ) 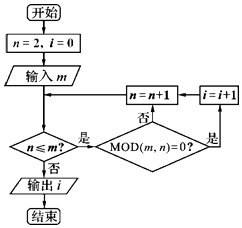
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com