
(本小题共14分)已知 是由满足下述条件的函数构成的集合:对任意
是由满足下述条件的函数构成的集合:对任意 ,①方程
,①方程 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 .
.
(Ⅰ)判断函数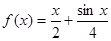 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(Ⅱ)集合 中的元素
中的元素 具有下面的性质:若
具有下面的性质:若 的定义域为
的定义域为 ,则对于任意
,则对于任意 ,都存在
,都存在 ,使得等式
,使得等式 成立.试用这一性质证明:方程
成立.试用这一性质证明:方程 有且只有一个实数根;
有且只有一个实数根;
(Ⅲ)对任意 ,且
,且 ,求证:对于
,求证:对于 定义域中任意的
定义域中任意的 ,
, ,
,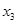 ,当
,当 ,且
,且 时,
时, .
.
解:(Ⅰ)因为①当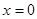 时,
时,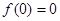 ,
,
所以方程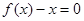 有实数根0;
有实数根0;
②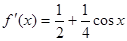 ,
,
所以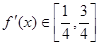 ,满足条件
,满足条件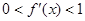 ;
;
由①②,函数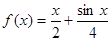 是集合
是集合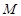 中的元素. …………5分
中的元素. …………5分
(Ⅱ)假设方程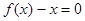 存在两个实数根
存在两个实数根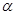 ,
,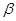
 ,
,
则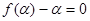 ,
, .
.
不妨设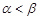 ,根据题意存在
,根据题意存在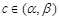 ,
,
满足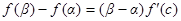 .
.
因为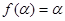 ,
,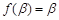 ,且
,且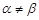 ,所以
,所以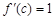 .
.
与已知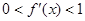 矛盾.又
矛盾.又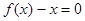 有实数根,
有实数根,
所以方程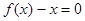 有且只有一个实数根. …………10分
有且只有一个实数根. …………10分
(Ⅲ)当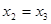 时,结论显然成立;
时,结论显然成立;
当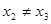 ,不妨设
,不妨设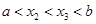 .
.
因为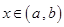 ,且
,且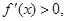 所以
所以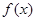 为增函数,那么
为增函数,那么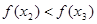 .
.
又因为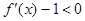 ,所以函数
,所以函数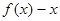 为减函数,
为减函数,
所以 .
.
所以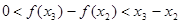 ,即
,即 .
.
因为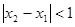 ,所以
,所以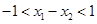 , (1)
, (1)
又因为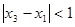 ,所以
,所以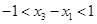 ,
(2)
,
(2)
(1)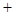 (2)得
(2)得 即
即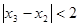 .
.
所以
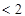 .
.
综上,对于任意符合条件的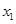 ,
,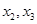 总有
总有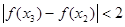 成立.……14分
成立.……14分
【解析】本题是一道以集合为背景的创新题,考查函数的性质和不等式的证明。考查学生的理解能力和分析能力。读懂题意是解题的前提,解题是注意分类讨论思想的应用。


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:
(08年北京卷文)(本小题共14分)
已知![]() 的顶点
的顶点![]() 在椭圆
在椭圆![]() 上,
上,![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(Ⅰ)当![]() 边通过坐标原点
边通过坐标原点![]() 时,求
时,求![]() 的长及
的长及![]() 的面积;
的面积;
(Ⅱ)当![]() ,且斜边
,且斜边![]() 的长最大时,求
的长最大时,求![]() 所在直线的方程.
所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题共14分)
已知双曲线![]() 的离心率为
的离心率为![]() ,右准线方程为
,右准线方程为![]()
(Ⅰ)求双曲线![]() 的方程;(Ⅱ)设直线
的方程;(Ⅱ)设直线![]() 是圆
是圆![]() 上动点
上动点![]() 处的切线,
处的切线,![]() 与双曲线
与双曲线![]() 交于不同的两点
交于不同的两点![]() ,证明
,证明![]() 的大小为定值..
的大小为定值..
查看答案和解析>>
科目:高中数学 来源:2010年北京市宣武区高三第二次模拟考试数学(理) 题型:解答题
(本小题共14分)
已知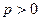 ,动点
,动点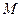 到定点
到定点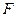
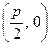 的距离比
的距离比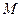 到定直线
到定直线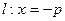 的距离小
的距离小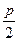 .
.
(I)求动点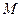 的轨迹
的轨迹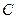 的方程;
的方程;
(Ⅱ)设 是轨迹
是轨迹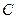 上异于原点
上异于原点 的两个不同点,
的两个不同点,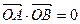 ,求
,求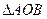 面积的最小值;
面积的最小值;
(Ⅲ)在轨迹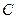 上是否存在两点
上是否存在两点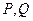 关于直线
关于直线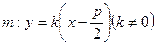 对称?若存在,求出直线
对称?若存在,求出直线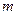 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年普通高中招生考试北京市高考理科数学 题型:解答题
((本小题共14分)
已知椭圆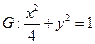 .过点(m,0)作圆
.过点(m,0)作圆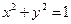 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点.
(I)求椭圆G的焦点坐标和离心率;
(II)将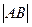 表示为m的函数,并求
表示为m的函数,并求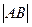 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市丰台区高三下学期统一练习数学理卷 题型:解答题
(本小题共14分)
已知点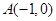 ,
,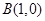 ,动点P满足
,动点P满足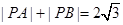 ,记动点P的轨迹为W.
,记动点P的轨迹为W.
(Ⅰ)求W的方程;
(Ⅱ)直线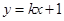 与曲线W交于不同的两点C,D,若存在点
与曲线W交于不同的两点C,D,若存在点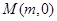 ,使得
,使得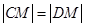 成立,求实数m的取值范围.
成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com