
【题目】如图, ![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() ,
, ![]() .将
.将![]() 沿
沿
![]() 折起,使
折起,使![]() 点与图中
点与图中![]() 点重合.
点重合.
(Ⅰ)求证:![]() ;
;
(Ⅱ)当三棱锥![]() 的体积取最大时,求二面角
的体积取最大时,求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在(Ⅱ)的条件下,试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?证明你的结论.
?证明你的结论.
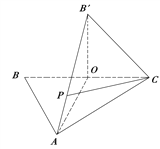
【答案】(Ⅰ)![]() 点,
点,
![]() 即
即![]() ,
,
又∵![]() ;
;
(Ⅱ)![]() ;(Ⅲ)存在,且为线段
;(Ⅲ)存在,且为线段![]() 的中点
的中点
证明如下:设![]() ,
,
![]()
又平面![]() 的法向量
的法向量![]() ,依题意得
,依题意得
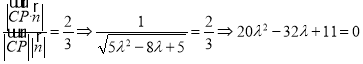
解得![]() 舍去).
舍去).
【解析】试题分析:(Ⅰ)欲证![]() ,需证明
,需证明![]() 垂直平面
垂直平面![]() 内两条直线,
内两条直线,
在三角形ABC中,因为![]() ,
, ![]() 是
是![]() 的中点,所以
的中点,所以![]() ;
;
又因为在折叠的过程中,![]() 保持不变,即
保持不变,即![]() ,
,![]() ,
,
所以结论成立;
(Ⅱ)在平面![]() 内,作
内,作![]() 于点
于点![]() ,则由(1)及已知可得当
,则由(1)及已知可得当![]() 与
与![]() 重合时,三棱锥
重合时,三棱锥![]() 的体积最大,并过
的体积最大,并过![]() 点作
点作![]() 于点
于点![]() ,连
,连![]() ,则
,则![]() 为
为![]()
在![]() 中,易得
中,易得![]() 的值,即为所求;
的值,即为所求;
(Ⅲ)根据图形及已知条件分析可得,存在线段![]() 上中点
上中点![]() ,使
,使![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求出平面
,求出平面![]() 的法向量
的法向量![]() ,根据
,根据![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() 建立等式关系,即可求得结论.
建立等式关系,即可求得结论.

试题解析:(Ⅰ) ![]() 点,
点,
![]() 即
即![]() ,
,
又∵![]() ;
;
(Ⅱ)在平面![]() 内,作
内,作![]() 于点
于点![]() ,则由(Ⅰ)可知
,则由(Ⅰ)可知![]()
又![]() ,
, ![]() ,即
,即![]() 是三棱锥
是三棱锥![]() 的高,
的高,
又![]() ,所以当
,所以当![]() 与
与![]() 重合时,三棱锥
重合时,三棱锥![]() 的体积最大,
的体积最大,
过![]() 点作
点作![]() 于点
于点![]() ,连
,连![]() ,由(Ⅰ)知
,由(Ⅰ)知
![]() ,
, ![]()
![]()
![]() 为
为![]()
![]() ,
, ![]()
![]()
(Ⅲ)存在,且为线段![]() 的中点
的中点
证明如下:设![]() ,
,
![]()
又平面![]() 的法向量
的法向量![]() ,依题意得
,依题意得
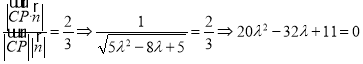
解得![]() 舍去).
舍去).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】给出下列命题:
①已知集合![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
③“函数![]() 的最小正周期为
的最小正周期为![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
④“平面向量![]() 与
与![]() 的夹角是钝角”的要条件是“
的夹角是钝角”的要条件是“![]() ”.
”.
其中正确命题的序号是 .(把所有正确命题的序号都写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取4个个体,选取方法从随机数表的第1行第4列数由左到右由上到下开始读取,则选出来的第4个个体的编号为( )
第1行 78 16 65 71 02 30 60 14 01 02 40 60 90 28 01 98
第2行 32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81
A.10B.01C.09D.06
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l、m 、n 与平面α、β给出下列四个命题:
①若m∥l,n∥l,则m∥n; ②若m⊥α,m∥β,则α⊥β;
③若m∥α,n∥α,则m∥n;④若m⊥β,α⊥β,则m∥α
其中,假命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的非负半轴为极轴建立极坐标,且两坐标系取相同的长度单位.已知点
轴的非负半轴为极轴建立极坐标,且两坐标系取相同的长度单位.已知点![]() 的极坐标为
的极坐标为![]() ,圆
,圆![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 为曲线
为曲线![]() 上的动点,且
上的动点,且![]() 到定点
到定点![]() 的距离等于圆
的距离等于圆![]() 的半径.
的半径.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为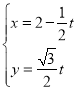 (
(![]() 为参数),且直线
为参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其![]() 下列叙述正确的是( )
下列叙述正确的是( )
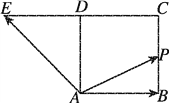
A. 满足λ+μ=2的点P必为BC的中点
B. 满足λ+μ=1的点P有且只有一个
C. λ+μ的最大值为3
D. λ+μ的最小值不存在
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题中:
①函数![]() 的一个对称中心为
的一个对称中心为![]() ;
;
②若![]() ,
, ![]() 为第一象限角,且
为第一象限角,且![]() ,则
,则![]() ;
;
③若![]() ,则存在实数
,则存在实数![]() ,使得
,使得![]() ;
;
④点![]() 是三角形
是三角形![]() 所在平面内一点,且满足
所在平面内一点,且满足![]() ,则点
,则点![]() 是三角形
是三角形![]() 的内心.
的内心.
其中正确的序号是__________.(把你认为正确的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com