
【题目】下列结论中错误的是( )
A.“﹣2<m<3”是方程![]() 表示椭圆”的必要不充分条件
表示椭圆”的必要不充分条件
B.命题p:![]() ,使得
,使得![]() 的否定
的否定![]()
![]()
C.命题“若![]() ,则方程
,则方程![]() 有实根”的逆否命题是真命题
有实根”的逆否命题是真命题
D.命题“若![]() ,则
,则![]() 且
且![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() 或
或![]() ”
”
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】经观测,某公路段在某时段内的车流量![]() (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度![]() (千米/小时)之间有函数关系:
(千米/小时)之间有函数关系:![]() .
.
(1)在该时段内,当汽车的平均速度![]() 为多少时车流量
为多少时车流量![]() 最大?最大车流量为多少?(精确到0.01)
最大?最大车流量为多少?(精确到0.01)
(2)为保证在该时段内车流量至少为10千辆/小时,则汽车的平均速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体中,四边形![]() 为菱形,对角线
为菱形,对角线![]() 与
与![]() 的交点为
的交点为![]() ,四边形
,四边形![]() 为梯形,
为梯形, ![]() .
.

(Ⅰ)若![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,
, ![]() ,求
,求![]() 与平面
与平面![]() 所成角.
所成角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的面积为
的面积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
,![]() 是
是![]() 上的两个动点,
上的两个动点,![]() ,试问:是否存在定点
,试问:是否存在定点![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在直角梯形ABCD中,AD=1,AD∥BC,AB⊥BC,BD⊥DC,点E是BC边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图②所示的几何体.
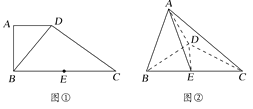
(1)求证:AB⊥平面ADC;
(2)若AC与平面ABD所成角的正切值为![]() ,求二面角B—AD—E的余弦值。
,求二面角B—AD—E的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:命题“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]() =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 中点(图1).将△
中点(图1).将△![]() 沿
沿![]() 折起,使得
折起,使得![]() (图2)在图2中:
(图2)在图2中:
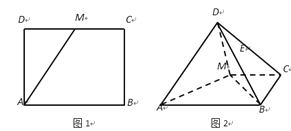
(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存点
上是否存点![]() ,使得二面角
,使得二面角![]() 为大小为
为大小为![]() ,说明理由.
,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人有楼房一幢,室内总面积为![]() ,拟分割成两类房间作为旅游客房,有关的数据如下表:
,拟分割成两类房间作为旅游客房,有关的数据如下表:
大房间 | 小房间 | |
每间的面积 |
|
|
每间装修费 |
| 6000元 |
每天每间住人数 | 5人 | 3人 |
每天每人住宿费 | 80元 | 100元 |
如果他只能筹款80000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,能获得的住宿总收入最多?每天获得的住宿总收入最多是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com