Question

4．已知函数f（x）=$\left\{\begin{array}{l}{|4-{x}^{2}|，x≤0}\\{{2}^{2-x}，0＜x≤2}\\{lo{g}_{2}x，x＞2}\end{array}\right.$，
（1）画出函数f（x）的图象；
（2）求f（f（3））的值；
（3）求f（a²+1）（a∈R）的最小值．

Answer 1

分析 （1）分段作图；
（2）求出f（3）的值，判断范围，进行二次迭代；
（3）求出a²+1的范围，根据图象得出结论．

解答 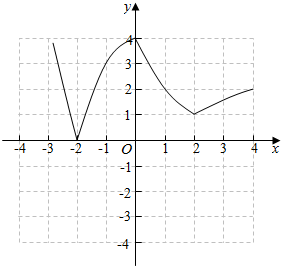解：（1）作出函数图象如右图所示，
（2）∵f（3）=log₂3，∴0＜f（3）＜2，
∴f（f（3））=f（log₂3）=2${\;}^{2-lo{g}_{2}3}$=$\frac{{2}^{2}}{{2}^{lo{g}_{2}3}}$=$\frac{4}{3}$．
（3）由函数图象可知f（x）在[1，2]上是减函数，在（2，+∞）上是增函数，
∵a²+1≥1，
∴当a²+1=2时，f（a²+1）取得最小值f（2）=1．

点评 本题考查了分段函数作图，函数求值及单调性，结合函数图象可快速得出结论．