Question

如图，在正四棱柱ABCD-A₁B₁C₁D₁中，已知AA₁=4，AB=2，E是棱CC₁上的一个动点．
（Ⅰ）求证：BE∥平面AA₁D₁D；
（Ⅱ）当CE=1时，求二面角B-ED-C的大小；
（Ⅲ）当CE等于何值时，A₁C⊥平面BDE．

Answer 1

分析：方法一：
（1）证明一条直线与一个平面平行，除了可以根据直线与平面平行的判定定理以外，通常还可以通过平面与平面平行进行转化，比如在正四棱柱ABCD-A₁B₁C₁D₁中，平面BB₁C₁C∥平面AA₁D₁D，BE?平面BB₁C₁C，所以BE∥平面AA₁D₁D．
（2）二面角的度量关键在于找出它的平面角，构造平面角常用的方法就是三垂线法．BC⊥平面C₁CDD₁，所以过C作CH⊥ED于H，连接BH，则∠BHC是二面角B-ED-C的平面角．
（3）由三垂线定理可知，A₁C⊥BD；故只需要在平面BDE再构造一条相交直线与A₁C垂直即可：连接B₁C，因为A₁B₁⊥平面B₁BCC₁，所以B₁C是A₁C在平面B₁BCC₁上的射影，由三垂线定理可知，只需B₁C⊥BE，则A₁C⊥BE
方法二：
以A为坐标原点，分别以AB、AD、AA₁为x、y、z轴，建立空间直角坐标系A-xyz．这种解法的好处就是：（1）解题过程中较少用到空间几何中判定线线、面面、线面相对位置的有关定理，因为这些可以用向量方法来解决．（2）即使立体感稍差一些的学生也可以顺利解出，因为只需画个草图以建立坐标系和观察有关点的位置即可．

解答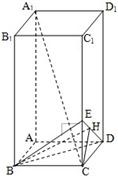：解：方法一：
（Ⅰ）证明：由已知，ABCD-A₁B₁C₁D₁为正四棱柱，
所以平面BB₁C₁C∥平面AA₁D₁D，
又因为BE?平面BB₁C₁C，
所以，BE∥平面AA₁D₁D．（4分）

（Ⅱ）解：如图，过C作CH⊥ED于H，连接BH．
因为ABCD-A₁B₁C₁D₁为正四棱柱，所以BC⊥平面C₁CDD₁．
则CH是斜线BH在面C₁CDD₁上的射影，所以BH⊥ED．
所以∠BHC是二面角B-ED-C的平面角．
在Rt△ECD中，易知CH•ED=EC•CD．
因为EC=1，CD=2，ED=

5

，所以CH=

2

5

．
在Rt△BCH中，tan∠BHC=

BC

CH

=

2

2 5

=

5

，所以∠BHC=arctan

5

，
所以，二面角B-ED-C的大小是arctan

5

．（9分）

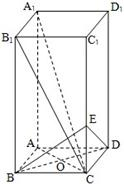
（Ⅲ）如图，连接AC交BD于点O，
因为ABCD-A₁B₁C₁D₁为正四棱柱，AC⊥BD，AA₁⊥平面ABCD，
由三垂线定理可知，A₁C⊥BD．
连接B₁C，因为A₁B₁⊥平面B₁BCC₁，
所以B₁C是A₁C在平面B₁BCC₁上的射影．
要使A₁C⊥平面BDE，只需A₁C⊥BE，由三垂线定理可知，只需B₁C⊥BE．
由平面几何知识可知，
B₁C⊥BE?△BCE∽△B₁BC?

CE

BC

=

BC

B1B

．
由已知BB₁=AA₁=4，BC=AB=2，所以CE=

BC2

B1B

=

22

4

=1．
即当CE=1时，A₁C⊥平面BDE．（14分）

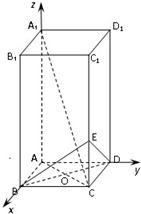
方法二：
建立空间直角坐标系A-xyz，如图．
（Ⅰ）证明：依题意可设E（2，2，z），
因为B（2，0，0），所以

BE

=（0，2，z）．
又因为

AB

=(2，0，0)，

AB

为平面AA₁D₁D的法向量．
且

BE

•

AB

=(2，0，0)•(0，2，z)=0，
所以

BE

⊥

AB

，而BE?平面AA₁D₁D，
所以，BE∥平面AA₁D₁D．

（Ⅱ）因为CE=1，所以E（2，2，1），又B（2，0，0），D（0，2，0），
所以

BE

=（0，2，1），

BD

=(-2，2，0)．
设平面BDE的法向量为

n

=(x，y，1)，
由

n• BE =0 n• BD =0

得

2y+1=0 -2x+2y=0

所以

x=- 1 2 y=- 1 2

所以n=(-

1

2

，-

1

2

，1)．又AD⊥面CC₁D₁D，所以

AD

为平面CDE的法向量．
因为

AD

=(0，2，0)，所以cos?n，

AD

?=

-1

4 • 1 4 + 1 4 +1

=-

6

6

．
由图可知，二面角的平面角小于90°，所以二面角B-ED-C的大小是arccos

6

6

．

（Ⅲ）解：连接AC交BD于点O．
因为ABCD-A₁B₁C₁D₁为正四棱柱，
所以AC⊥BD．
要使A₁C⊥平面BDE，只需A₁C⊥BE．
由题意B（2，0，0），C（2，2，0），A₁（0，0，4），
设CE=x，则E（2，2，x），
所以

BE

=(0，2，x)，

A1C

=(2，2，-4)．
由

BE

•

A1C

=0，得（0，2，x）•（2，2，-4）=0×2+2×2+x×（-4）=4-4x=0，
解得x=1．所以CE=1时，A₁C⊥平面BDE．

点评：本小题主要考查空间线面关系、二面角的度量等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．