
【题目】已知定义在区间(0,+∞)上的函数f(x)=|t(x+ ![]() )﹣5|,其中常数t>0.
)﹣5|,其中常数t>0.
(1)若函数f(x)分别在区间(0,2),(2,+∞)上单调,试求实数t的取值范围;
(2)当t=1时,方程f(x)=m有四个不相等的实根x1 , x2 , x3 , x4 . ①求四根之积x1x2x3x4的值;
②在[1,4]上是否存在实数a,b(a<b),使得f(x)在[a,b]上单调且取值范围为[ma,mb]?若存在,求出m的取值范围;若不存在,请说明理由.
【答案】
(1)解:设h(x)=t(x+ ![]() )
)
∵t>0,
∴函数h(x)在区间(0,2),(2,+∞)上单调,且h(x)≥4t,
要使函数f(x)分别在区间(0,2),(2,+∞)上单调,
只需4t﹣5≥0,
∴t≥ ![]()
(2)解:①当t=1 时,由f(x)=m得|(x+ ![]() )﹣5|=m,
)﹣5|=m,
∴(x+ ![]() )﹣5=m,或(x+
)﹣5=m,或(x+ ![]() )﹣5=﹣m,
)﹣5=﹣m,
即x2﹣(m+5)x+4=0,或x2+(m+5)x+4=0
∵x1,x2,x3,x4是方程f(x)=m的四个不相等的实根,
∴x1x2x3x4=4×4=16
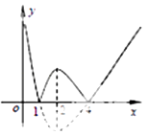
②f(x)在区间(0,1),(1,2),(2,4),(4,+∞)上均为单调函数
(i)当[a,b](1,2]时,f(x)在[a,b]上单调递增,则 ![]()
即m= ![]() 在a∈(1,2]时,有两个不等实根
在a∈(1,2]时,有两个不等实根
而令 ![]() ,则
,则 ![]() =φ(t)=﹣4(t﹣
=φ(t)=﹣4(t﹣ ![]() )2+
)2+ ![]() ,
,
则φ(t)=﹣4(t﹣ ![]() )2+
)2+ ![]() =m在[
=m在[ ![]() ,1)上有两个根,
,1)上有两个根,
由当t= ![]() 时,函数φ(t)取最大值
时,函数φ(t)取最大值 ![]() ,
,
当t= ![]() 时,φ(
时,φ( ![]() )=
)= ![]() ,当t=1时,φ(1)=0,
,当t=1时,φ(1)=0,
故 ![]()
(ii)当[a,b](2,4]时,f(x)在[a,b]上单调递减,则 ![]() 两式相除得(a﹣b)(a+b﹣5)=0
两式相除得(a﹣b)(a+b﹣5)=0
∴a+b=5,
∴b=5﹣a>a,
∴2<a< ![]() ,
,
由﹣a﹣ ![]() +5=mb得:m=
+5=mb得:m= ![]() =1+
=1+ ![]() ∈(
∈( ![]() ,
, ![]() ),
),
综上,m的取值范围为( ![]() ,
, ![]() )
)
【解析】(1)设h(x)=t(x+ ![]() )结合对勾函数的图像和性质,可得函数h(x)在区间(0,2),(2,+∞)上单调,且h(x)≥4t,要使函数f(x)分别在区间(0,2),(2,+∞)上单调,只需4t﹣5≥0,解得:实数t的取值范围;(2)当t=1时,由f(x)=m得|(x+
)结合对勾函数的图像和性质,可得函数h(x)在区间(0,2),(2,+∞)上单调,且h(x)≥4t,要使函数f(x)分别在区间(0,2),(2,+∞)上单调,只需4t﹣5≥0,解得:实数t的取值范围;(2)当t=1时,由f(x)=m得|(x+ ![]() )﹣5|=m,即(x+
)﹣5|=m,即(x+ ![]() )﹣5=m,或(x+
)﹣5=m,或(x+ ![]() )﹣5=﹣m,即x2﹣(m+5)x+4=0,或x2+(m+5)x+4=0, ①由韦达定理,可得四根之积x1x2x3x4的值;
)﹣5=﹣m,即x2﹣(m+5)x+4=0,或x2+(m+5)x+4=0, ①由韦达定理,可得四根之积x1x2x3x4的值;
②f(x)在区间(0,1),(1,2),(2,4),(4,+∞) 上均为单调函数,(1)当[a,b](1,2]时,f(x)在[a,b]上单调递增,则 ![]() ;(2)当[a,b](2,4]时,f(x)在[a,b]上单调递减,则
;(2)当[a,b](2,4]时,f(x)在[a,b]上单调递减,则 ![]() ;综合讨论结果,可得m的取值范围.
;综合讨论结果,可得m的取值范围.
【考点精析】利用函数单调性的判断方法和函数单调性的性质对题目进行判断即可得到答案,需要熟知单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=log2(4x)log2(2x)的定义域为 ![]() . (Ⅰ)若t=log2x,求t的取值范围;
. (Ⅰ)若t=log2x,求t的取值范围;
(Ⅱ)求y=f(x)的最大值与最小值,并求取得最值时对应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
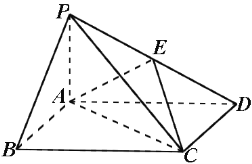
【题目】【2014高考课标2理数18】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,
E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积.
,求三棱锥E-ACD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的身体素质情况,现从我校学生中随机抽取10人进行体能测试,测试的分数(百分制)如茎叶图所示.根据有关国家标准,成绩不低于79分的为优秀,将频率视为概率.
(1)另从我校学生中任取3人进行测试,求至少有1人成绩是“优秀”的概率;
(2)从前文所指的这10人(成绩见茎叶图)中随机选取3人,记![]() 表示测试成绩为“优秀”的学生人数,求
表示测试成绩为“优秀”的学生人数,求![]() 的分布列及期望.
的分布列及期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
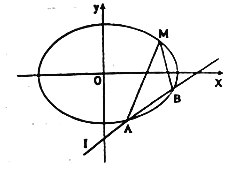
【题目】已知椭圆的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,且经过点
,且经过点![]() ,直线
,直线![]() :
: ![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两不同的点.
两不同的点.
(1)求椭圆的方程;
(2)若直线![]() 不过点
不过点![]() ,求证:直线
,求证:直线![]() ,
, ![]() 与
与![]() 轴围成等腰三角形.
轴围成等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄”45岁为分界点,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在![]() 和
和![]() 的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在
的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在![]() 的概率.
的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: 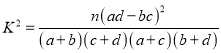 (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(3﹣ax)(a>0,a≠1)
(1)当a=3时,求函数f(x)的定义域;
(2)若g(x)=f(x)﹣loga(3+ax),请判定g(x)的奇偶性;
(3)是否存在实数a,使函数f(x)在[2,3]递增,并且最大值为1,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题,其中正确的个数有( )
①由独立性检验可知,有![]() 的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在线性回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
④对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说, ![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com