【题目】平面内有向量 
=（1，7）， 
=（5，1）， 
=（2，1），点X为直线OP上的一个动点．
（1）当 
取最小值时，求 
的坐标；
（2）当点X满足（1）的条件和结论时，求cos∠AXB的值．
【答案】
（1）解：设 
=（x，y），
∵点X在直线OP上，∴向量 与 
共线．
又 =（2，1），∴x﹣2y=0，即x=2y．
∴ =（2y，y）．又 
= 
﹣ ， =（1，7），
∴ =（1﹣2y，7﹣y）．
同样 
= 
﹣ =（5﹣2y，1﹣y）．
于是 =（1﹣2y）（5﹣2y）+（7﹣y）（1﹣y）=5y2﹣20y+12=5（y﹣2）2﹣8．
∴当y=2时， 有最小值﹣8，此时 =（4，2）
（2）解：当 =（4，2），即y=2时，有 =（﹣3，5）， =（1，﹣1）．
∴| |= 
，| |= 
．
∴cos∠AXB=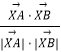 
=﹣ 
【解析】（1）因为点X在直线OP上，向量 与 共线，可以得到关于 坐标的一个关系式，再根据 的最小值，求得 的坐标，（2）cos∠AXB是 与 夹角的余弦，利用数量积的知识易解决．
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案科目：高中数学 来源： 题型：
【题目】如图， 
是半圆
的直径， 
是半圆
上除
、
外的一个动点， 
垂直于半圆
所在的平面， 
， 
， 
， 
.
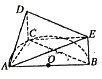
（1）证明：平面
平面
；
（2）当三棱锥
体积最大时，求二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在四棱柱
中， 
底面
，底面
为菱形， 
为
与
交点，已知
,
.
（Ⅰ）求证： 
平面
；
（Ⅱ）求证： 
∥平面
；
（Ⅲ）设点
在
内（含边界）,且
，说明满足条件的点
的轨迹，并求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}，{bn}满足a1=1，且an ， an+1是函数f（x）=x2﹣bnx+2n的两个零点，则b10等于（ ）
A.24
B.32
C.48
D.64
查看答案和解析>>
科目：高中数学 来源： 题型：
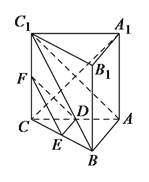
【题目】如图，在三棱柱
中，
底面
，
，
、
分别是棱
、
的中点．
（Ⅰ）求证：
平面
．
（Ⅱ）若线段
上的点
满足平面
平面
，试确定点的位置，并说明理由．
（Ⅲ）证明：
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|cosx|sinx，给出下列四个说法：
①f（x）为奇函数； ②f（x）的一条对称轴为x= 
；
③f（x）的最小正周期为π； ④f（x）在区间[﹣ 
， ]上单调递增；
⑤f（x）的图象关于点（﹣ ，0）成中心对称．
其中正确说法的序号是 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
