练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．若$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，-2），$\overrightarrow{c}$=（2，1），则（$\overrightarrow{a}$•$\overrightarrow{b}$）$\overrightarrow{c}$=（-16，-8），$\overrightarrow{a}$（$\overrightarrow{b}$•$\overrightarrow{c}$）=（-8，-12）．

    分析 利用平面向量的数量积和数乘的坐标运算解答．

    解答 解：$\overrightarrow{a}$=（2，3），$\overrightarrow{b}$=（-1，-2），$\overrightarrow{c}$=（2，1），则（$\overrightarrow{a}$•$\overrightarrow{b}$）$\overrightarrow{c}$=-8（2，1）=（-16，-8），
    $\overrightarrow{a}$（$\overrightarrow{b}$•$\overrightarrow{c}$）=-4（2，3）=（-8，-12）；
    故答案为：（-16，-8）；（-8，-12）．

    点评 本题考查了平面向量的数量积和数乘的坐标运算，注意运算法则的运用；属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．已知集合A={x|0＜x＜3}，B={x|-1＜x＜3}，则A∪B=（　　）
    A．{x|-1＜x＜3}B．{x|0＜x＜3}C．{x|x＞-1}D．{x|x＜3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知P为△ABC所在平面内一点，且满足$\overrightarrow{AP}$=$\frac{1}{5}$$\overrightarrow{AC}$+$\frac{2}{5}$$\overrightarrow{AB}$，则△APB的面积与△APC的面积之比为（　　）
    A．$\frac{1}{2}$B．2C．$\frac{1}{3}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

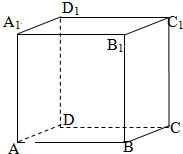    17．ABCD-A1B1C1D1是单位正方体，黑白两只蚂蚁从点A出发沿棱向前爬行，每爬完一条棱称为“爬完一段”．白蚂蚁爬行的路线是AA1→A1D1，…，黑蚂蚁爬行的路线是AB→BB1，…，它们都遵循如下规则：所爬行的第i+2段与第i段所在直线必须是异面直线（i∈N*），设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处，则此时黑白蚂蚁的距离是（　　）
    A．$\sqrt{2}$B．1C．0D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．有两个不透明的箱子，每个箱子里都装有3个完全相同的小球，球上分别标有数字1，2，3．甲从其中一个箱子中随机摸出一个球，乙从另一个箱子中随机摸出一个球，谁摸出的球上标的数字大谁就获胜（若数字相同则为平局），则甲没有获胜的概率为$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知数列{an}的前n项和为Sn，且Sn=2n+1-2，数列{bn}满足b1=1，bn+1=bn+2，n∈N*．
    （1）求数列{an}、{bn}的通项公式；
    （2）若cn=anbn，n∈N*，求数列{cn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．函数y=$\frac{x}{{x}^{2}+1}$的图象与函数y=sin$\frac{π}{2}$x（-5≤x≤5）的图象所有交点的横坐标之和等于（　　）
    A．0B．4C．10D．2π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．数列{an}的前n项和为Sn，且满足a1=1，2Sn=（n+1）an．
    （1）求数列{an}的通项公式；
    （2）求和Tn=$\frac{1}{{{a}_{2}}^{2}-1}$+$\frac{1}{{{a}_{3}}^{2}-1}$+$\frac{1}{{{a}_{4}}^{2}-1}$+…+$\frac{1}{{{a}_{n+1}}^{2}-1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．从装有4个红球和3个黑球的口袋内任取3个球，那么互斥而不对立的事件是（　　）
    A．至少有一个红球与都是黑球B．至少有一个红球与恰有一个黑球
    C．至少有一个红球与至少有一个黑球D．恰有一个红球与恰有两个红球

    查看答案和解析>>

    同步练习册答案