
一个数列中的数均为奇数时,称之为“奇数数列”. 我们给定以下法则来构造一个奇数数列{an},对于任意正整数n,当n为奇数时,an=n;当n为偶数时,an=![]() .
.
(1)试写出该数列的前6 项;
(2)研究发现,该数列中的每一个奇数都会重复出现,那么第10个5是该数列的第几项?
(3)求该数列的前2n项的和Tn.
解:(1)a1=1,a2=1,a3=3,a4=1,a5=5,a6=3.
(2)第1个5出现在第5项,第2个5出现在第2×5=10项,第3个5出现在第22×5=20项,第4个5出现在第23×5=40项,依次类推.
第10个5是该数列的第29×5=2560项.
(3)Tn= a1+a2+a3+a4+a5+a6+…+![]()
=(a1+a3+a5+…+![]() )+(a2+a4+a6+…+
)+(a2+a4+a6+…+![]() )
)
=(1+3+5+7+…+(2n-1)+(a1+a2+a3+…+![]() )
)
=4n-1+Tn-1 (n≥ 2)
用累加法得:Tn=T1+4+42+…+4n-1=![]() (n ≥ 2)
(n ≥ 2)
当n=1时,T1=2=![]()
∴对一切正整数n都有Tn= ![]() .
.


科目:高中数学 来源: 题型:
| n | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n | 2 |
查看答案和解析>>
科目:高中数学 来源:湖南省模拟题 题型:解答题
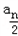 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com