
分析 求解对数不等式化简A.
(1)直接由补集运算得答案;
(2)直接由集合间的关系求得a的范围;
(3)分C为∅和非空集合讨论,当≠∅时,由集合间的关系列不等式组求解.
解答 解:由lg($\frac{2x-5}{x+2}$)≤0,得0<$\frac{2x-5}{x+2}$≤1,解得:$\frac{5}{2}<x≤7$.
(1)A={x|lg($\frac{2x-5}{x+2}$)≤0}={x|$\frac{5}{2}<x≤7$},又U=R,
∴∁UA={x|x$≤\frac{5}{2}$或x>7};
(2)∵A={x|$\frac{5}{2}<x≤7$},B={x|x<a},
若A⊆B,则a>7;
(3)C={x|m+1≤x≤2m-1},
由C⊆A,若m+1>2m-1,即m<2,C=∅,符合题意;
当m≥2时,要使C⊆A,则$\left\{\begin{array}{l}{m+1>\frac{5}{2}}\\{2m-1≤7}\end{array}\right.$,解得:$\frac{3}{2}<m≤4$.
∴2≤m≤4.
综上,m≤4.
点评 本题考查分式不等式的解法,考查了交、并、补集的混合运算,考查集合间的关系及其应用,关键是对集合端点值间关系的处理,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
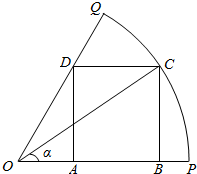 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分必要条件 | B. | 充分条件但非必要条件 | ||
| C. | 必要条件但非充分条件 | D. | 既非充分条件又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(3)<f(-4)<f(-π) | B. | f(-π)<f(-4)<f(3) | C. | f(-4)<f(-π)<f(3) | D. | f(3)<f(-π)<f(-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com