
【题目】北京市环境保护监测中心每月向公众公布北京市各区域的空气质量状况![]() 年1月份各区域的
年1月份各区域的![]() 浓度情况如表:
浓度情况如表:
各区域1月份![]() 浓度
浓度![]() 单位:微克
单位:微克![]() 立方米
立方米![]() 表
表
区域 |
| 区域 |
| 区域 |
|
怀柔 | 27 | 海淀 | 34 | 平谷 | 40 |
密云 | 31 | 延庆 | 35 | 丰台 | 42 |
门头沟 | 32 | 西城 | 35 | 大兴 | 46 |
顺义 | 32 | 东城 | 36 | 开发区 | 46 |
昌平 | 32 | 石景山 | 37 | 房山 | 47 |
朝阳 | 34 | 通州 | 39 |
从上述表格随机选择一个区域,其2018年1月份![]() 的浓度小于36微克
的浓度小于36微克![]() 立方米的概率是
立方米的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】若命题p:从有2件正品和2件次品的产品中任选2件得到都是正品的概率为三分之一;命题q:在边长为4的正方形ABCD内任取一点M,则∠AMB>90°的概率为 ![]() ,则下列命题是真命题的是( )
,则下列命题是真命题的是( )
A.p∧q
B.(p)∧q
C.p∧(q)
D.q
查看答案和解析>>
科目:高中数学 来源: 题型:
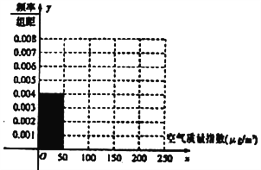
【题目】全世界越来越关注环境保护问题,某监测站点于2018年1月某日起连续![]() 天监测空气质量指数(
天监测空气质量指数(![]() ),数据统计如下:
),数据统计如下:
空气质量指数( |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 |
| 10 | 5 |
(1)根据所给统计表和频率分布直方图中的信息求出![]() ,
,![]() 的值,并完成频率分布直方图;
的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的众数和中位数;
(3)在空气质量指数分别属于![]() 和
和![]() 的监测数据中,用分层抽样的方法抽取
的监测数据中,用分层抽样的方法抽取![]() 天,再从中任意选取
天,再从中任意选取![]() 天,求事件
天,求事件![]() “两天空气都为良”发生的概率.
“两天空气都为良”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|cosx|sinx,给出下列五个说法:
①f( ![]() π)=﹣
π)=﹣ ![]() ;
;
②若|f(x1)|=|f(x2)|,则x1=x2+kπ(k∈Z);
③f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递增;
]上单调递增;
④函数f(x)的周期为π.
⑤f(x)的图象关于点( ![]() ,0)成中心对称.
,0)成中心对称.
其中正确说法的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】种植于道路两侧、为车辆和行人遮阴并构成街景的乔木称为行道树![]() 为确保行人、车辆和临近道路附属设施安全,树木与原有电力线之间的距离不能超出安全距离
为确保行人、车辆和临近道路附属设施安全,树木与原有电力线之间的距离不能超出安全距离![]() 按照北京市
按照北京市![]() 行道树修剪规范
行道树修剪规范![]() 要求,当树木与原有电力线发生矛盾时,应及时修剪树枝
要求,当树木与原有电力线发生矛盾时,应及时修剪树枝![]() 行道树修剪规范
行道树修剪规范![]() 中规定,树木与原有电力线的安全距离如表所示:树木与电力线的安全距离表
中规定,树木与原有电力线的安全距离如表所示:树木与电力线的安全距离表
电力线 | 安全距离 | |
水平距离 | 垂直距离 | |
|
|
|
|
|
|
|
|
|
|
|
|
330KV |
|
|
500KV |
|
|
现有某棵行道树已经自然生长2年,高度为![]() 据研究,这种行道树自然生长的时间
据研究,这种行道树自然生长的时间![]() 年
年![]() 与它的高度
与它的高度![]() 满足关系式
满足关系式![]()
![]() 1
1![]() ______;
______;![]() 将结果直接填写在答题卡的相应位置上
将结果直接填写在答题卡的相应位置上![]()
![]() 2
2![]() 如果这棵行道树的正上方有35kV的电力线,该电力线距地面
如果这棵行道树的正上方有35kV的电力线,该电力线距地面![]() 那么这棵行道树自然生长多少年必须修剪?
那么这棵行道树自然生长多少年必须修剪?
![]() 3
3![]() 假如这棵行道树的正上方有500KV的电力线,这棵行道树一直自然生长,始终不会影响电力线段安全,那么该电力线距离地面至少多少米?
假如这棵行道树的正上方有500KV的电力线,这棵行道树一直自然生长,始终不会影响电力线段安全,那么该电力线距离地面至少多少米?
查看答案和解析>>
科目:高中数学 来源: 题型:
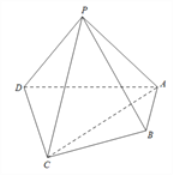
【题目】如图,在四棱锥![]() 中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,
中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2, ![]() .
.
(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,点
,点![]() 在椭圆上,A,B分别为椭圆的右顶点与上顶点,过点A,B引椭圆C的两条弦AE、BF交椭圆于点E,F.
在椭圆上,A,B分别为椭圆的右顶点与上顶点,过点A,B引椭圆C的两条弦AE、BF交椭圆于点E,F.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 若直线AE,BF的斜率互为相反数,
若直线AE,BF的斜率互为相反数,
![]() 求出直线EF的斜率;
求出直线EF的斜率;
![]() 若O为直角坐标原点,求
若O为直角坐标原点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com