
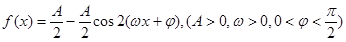 的图象过点(1,2),相邻两条对称轴间的距离为2,且
的图象过点(1,2),相邻两条对称轴间的距离为2,且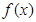 的最大值为2.
的最大值为2.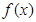 的单调递增区间;
的单调递增区间;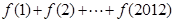 ;
;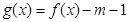 ,试讨论函数
,试讨论函数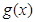 在区间[1,4]上的零点情况.
在区间[1,4]上的零点情况.

 见解析(Ⅲ)
见解析(Ⅲ) ,再根据图像过点(1,2),
,再根据图像过点(1,2), .从而确定f(x)的表达式进而可求出其单调增区间.
.从而确定f(x)的表达式进而可求出其单调增区间. ,
,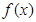 的最大值为2且A>0,
的最大值为2且A>0, 即A=2
即A=2 ,又函数
,又函数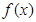 的图象过点(1,2)则
的图象过点(1,2)则

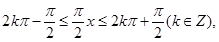 得
得
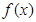 的单调增区间是
的单调增区间是
 .
. ,
,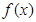 的周期为4,而2012=4×503
的周期为4,而2012=4×503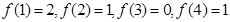


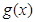 的零点个数即为函数
的零点个数即为函数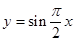 的图象与直线
的图象与直线 的交点个数.然后分别作出其图像,从图像上观察得到结论即可.
的交点个数.然后分别作出其图像,从图像上观察得到结论即可.
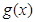 的零点个数即为函数
的零点个数即为函数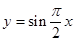 的图象与直线
的图象与直线 的交点个数.
的交点个数.
 或
或 时,函数
时,函数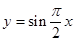 的图象与直线
的图象与直线 无公共点,即函数
无公共点,即函数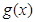 无零点;
无零点;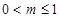 或
或 时,函数
时,函数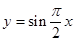 的图象与
的图象与 有一个公共点,即函数
有一个公共点,即函数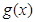 有一个零点;
有一个零点; 时,函数
时,函数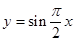 的图象与
的图象与 有两个公共点,即函数
有两个公共点,即函数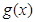 有两个零点.
有两个零点.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源:不详 题型:解答题
 为单位圆在第一象限内圆弧上的动点,
为单位圆在第一象限内圆弧上的动点, ,设
,设 ,过
,过 作直线
作直线 ,并交直线
,并交直线 于点
于点 .
.
 的坐标 (用
的坐标 (用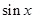 表示) ;
表示) ; 能否为
能否为 ?若能,求出点
?若能,求出点 的坐标,若不能,请说明理由.
的坐标,若不能,请说明理由. 的面积的最大值,并求出相应
的面积的最大值,并求出相应 值.
值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com