练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某校组织甲、乙、丙、丁、戊、己等6名学生参加演讲比赛，采用抽签法决定演讲顺序，在“学生甲和乙都不是第一个出场，且甲不是最后一个出场”的前提下，学生丙第一个出场的概率为__________．

    【答案】

    【解析】

    由条件概率计算方式，分别计算事件A：“学生甲和乙都不是第一个出场，且甲不是最后一个出场”的基本事件个数，其中分两类乙在最后与乙不在最后计数，与事件AB的基本事件个数，最后由公式求解即可.

    设事件A：“学生甲和乙都不是第一个出场，且甲不是最后一个出场”；事件B：“学生丙第一个出场”，

    对事件A，甲和乙都不是第一个出场，第一类：乙在最后，则优先从中间4个位置中选一

    个给甲，再将余下的4个人全排列有种；第二类：乙没有在最后，则优先从中间4

    个位置中选两个给甲乙，再将余下的4个人全排列有种，故总的有.

    对事件AB，此时丙第一个出场，优先从除了甲以外的4人中选一人安排在最后，再将余下的4人全排列有种

    故.

    故答案为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆中心在原点，焦点在坐标轴上，直线与椭圆在第一象限内的交点是，点在轴上的射影恰好是椭圆的右焦点，椭圆另一个焦点是，且.

    （1）求椭圆的方程；

    （2）直线过点，且与椭圆交于两点，求的内切圆面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知下列命题：

    ①在线性回归模型中，相关指数越接近于1，表示回归效果越好；

    ②两个变量相关性越强，则相关系数r就越接近于1；

    ③在回归直线方程中，当解释变量每增加一个单位时，预报变量平均减少0.5个单位；

    ④两个模型中残差平方和越小的模型拟合的效果越好.

    ⑤回归直线恒过样本点的中心，且至少过一个样本点；

    ⑥若的观测值满足≥6.635，我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病；

    ⑦从统计量中得知有95%的把握认为吸烟与患肺病有关系，是指有5%的可能性使得推断出现错误． 其中正确命题的序号是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某机构对某市工薪阶层的收入情况与超前消费行为进行调查，随机抽查了200人，将他们的月收入（单位：百元）频数分布及超前消费的认同人数整理得到如下表格：

    月收入（百元）

    频数

    20

    40

    60

    40

    20

    20

    认同超前消费的人数

    8

    16

    28

    21

    13

    16

    （1）根据以上统计数据填写下面列联表，并回答是否有99%的把握认为当月收入以8000元为分界点时，该市的工薪阶层对“超前消费”的态度有差异；

    月收入不低于8000元

    月收入低于8000元

    总计

    认同

    不认同

    总计

    （2）若从月收入在的被调查对象中随机选取2人进行调查，求至少有1个人不认同“超前消费”的概率.

    参考公式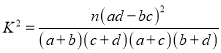：（其中）.

    附表：

    0.10

    0.05

    0.025

    0.010

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形为正方形，四边形为矩形，且平面与平面互相垂直．若多面体的体积为，则该多面体外接球表面积的最小值为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

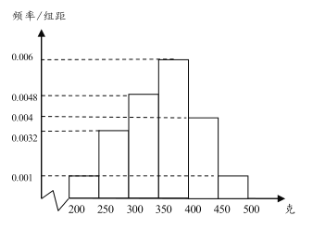
    【题目】经过多年的努力，炎陵黄桃在国内乃至国际上逐渐打开了销路，成为炎陵部分农民脱贫致富的好产品.为了更好地销售，现从某村的黄桃树上随机摘下了100个黄桃进行测重，其质量分布在区间内（单位：克），统计质量的数据作出其频率分布直方图如图所示：

    （1）按分层抽样的方法从质量落在，的黄桃中随机抽取5个，再从这5个黄桃中随机抽2个，求这2个黄桃质量至少有一个不小于400克的概率；

    （2）以各组数据的中间数值代表这组数据的平均水平，以频率代表概率，已知该村的黄桃树上大约还有100000个黄桃待出售，某电商提出两种收购方案：

    A.所有黄桃均以20元/千克收购；

    B.低于350克的黄桃以5元/个收购，高于或等于350克的以9元/个收购.

    请你通过计算为该村选择收益最好的方案.

    （参考数据：）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝，其中a为常数．

    （1）当a＝1时，求f（x）的最大值；

    （2）若f（x）在区间(0，e]上的最大值为－2，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A＝{x|x＝6n﹣1，n∈N*}，B＝{x|x＝2n，n∈N*}，将A∪B的所有元素从小到大依次排列构成一个数列{an}．记Sn为数列{an}的前n项和，若Sm＝3014，则正整数m值为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地区某农产品近几年的产量统计如表：

    年份

    2012

    2013

    2014

    2015

    2016

    2017

    年份代码t

    1

    2

    3

    4

    5

    6

    年产量y(万吨)

    6.6

    6.7

    7

    7.1

    7.2

    7.4

    （Ⅰ）根据表中数据，建立关于的线性回归方程；

    （Ⅱ）根据线性回归方程预测2019年该地区该农产品的年产量.

    附:对于一组数据，其回归直线的斜率和截距的最小二乘估计分别为：，.(参考数据:，计算结果保留小数点后两位）

    查看答案和解析>>

    同步练习册答案