
【题目】在△ABC中,角A、B、C所对的边分别为a、b、c,f (x)=sin(2x﹣A) (x∈R),函数f(x)的图象关于点( ![]() ,0)对称.
,0)对称.
(1)当x∈(0, ![]() )时,求f (x)的值域;
)时,求f (x)的值域;
(2)若a=7且sinB+sinC= ![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】
(1)解:∵函数f(x)的图象关于点( ![]() ,0)对称,
,0)对称,
∴f( ![]() )=0,即sin(2×
)=0,即sin(2× ![]() ﹣A)=0.
﹣A)=0.
又A∈(0,π),
∴A= ![]() .
.
∵x∈(0, ![]() ),
),
∴2x﹣ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ),
),
∴﹣ ![]() <sin(2x﹣
<sin(2x﹣ ![]() )≤1,
)≤1,
即函数f(x)的值域为(﹣ ![]() ,1].
,1].
(2)解:由正弦定理 ![]() ,
,
得sinB+sinC= ![]() +
+ ![]() ,
,
又∵a=7,A= ![]() ,
,
∴sinB+sinC= ![]() (b+c).
(b+c).
∵sinB+sinC= ![]() ,
,
∴b+c=13.
由余弦定理a2=b2+c2﹣2bccosA,
得49=b2+c2﹣bc,
即49=(b+c)2﹣3bc=169﹣3bc,
∴bc=40.
∴S△ABC= ![]() bcsinA=10
bcsinA=10 ![]() .
.
【解析】(1)由题意sin(2× ![]() ﹣A)=0,结合A∈(0,π),可得A=
﹣A)=0,结合A∈(0,π),可得A= ![]() ,由x∈(0,
,由x∈(0, ![]() ),可求2x﹣
),可求2x﹣ ![]() 的范围,利用正弦函数的图象和性质即可得解f(x)的值域.(2)由正弦定理得sinB+sinC=
的范围,利用正弦函数的图象和性质即可得解f(x)的值域.(2)由正弦定理得sinB+sinC= ![]() +
+ ![]() ,结合已知可求b+c=13,利用余弦定理可求bc的值,利用三角形面积公式即可得解.
,结合已知可求b+c=13,利用余弦定理可求bc的值,利用三角形面积公式即可得解.
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义,掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面四边形ABCD是菱形,
中,底面四边形ABCD是菱形, ![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() ,
, ![]() .
.
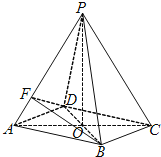
![]() Ⅰ
Ⅰ![]() 求证:
求证: ![]() 底面ABCD;
底面ABCD;
![]() Ⅱ
Ⅱ![]() 求直线CP与平面BDF所成角的大小;
求直线CP与平面BDF所成角的大小;
![]() Ⅲ
Ⅲ![]() 在线段PB上是否存在一点M,使得
在线段PB上是否存在一点M,使得![]() 平面BDF?如果存在,求
平面BDF?如果存在,求![]() 的值,如果不存在,请说明理由.
的值,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() =
=
(1)写出该函数的单调区间;
(2)若函数![]() =
=![]() -m恰有3个不同零点,求实数m的取值范围;
-m恰有3个不同零点,求实数m的取值范围;
(3)若![]() ≤n2-2bn+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数n的取值范围.
≤n2-2bn+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱垂直于底面,
中,侧棱垂直于底面, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:在棱![]() 上存在一点
上存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D两点.
(1)若p=2且∠BFD=90°时,求圆F的方程;
(2)若A,B,F三点在同一直线m上,设直线m与抛物线C的另一个交点为E,在y轴上求一点G,使得∠OGE=∠OGA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,短轴右端点为
,短轴右端点为![]() ,
, ![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ) 求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 任作一条直线与椭圆
任作一条直线与椭圆![]() 相交于两点
相交于两点![]() ,试探究在
,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com