
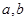 ,定义
,定义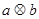 的算法原理如右侧程序框图所示.设
的算法原理如右侧程序框图所示.设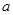 为函数
为函数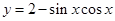 的最大值,
的最大值,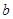 为双曲线
为双曲线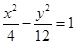 的离心率,则计算机执行该运算后输出的结果是( )
的离心率,则计算机执行该运算后输出的结果是( )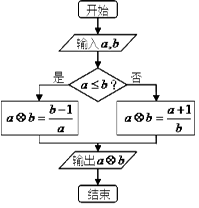
A.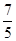 | B.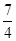 | C.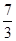 | D.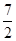 |
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源:不详 题型:解答题
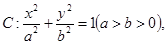 动直线
动直线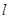 与椭圆
与椭圆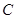 只有一个公共点
只有一个公共点 ,且点
,且点 在第一象限.
在第一象限.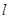 的斜率为
的斜率为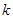 ,用
,用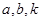 表示点
表示点 的坐标;
的坐标;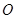 的直线
的直线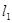 与
与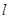 垂直,证明:点
垂直,证明:点 到直线
到直线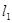 的距离的最大值为
的距离的最大值为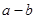 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
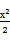 -y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
-y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.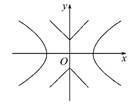
 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
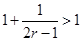 ,
,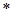 ,
,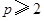 ,
, 分别是椭圆
分别是椭圆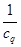 的四个顶点,△
的四个顶点,△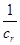 是一个边长为2的等边三角形,其外接圆为圆
是一个边长为2的等边三角形,其外接圆为圆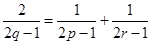 .
.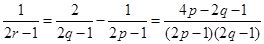 及圆
及圆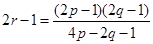 的方程;
的方程;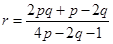 是圆
是圆 劣弧
劣弧 上一动点(点
上一动点(点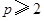 异于端点
异于端点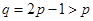 ,
,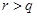 ),直线
),直线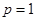 分别交线段
分别交线段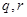 ,椭圆
,椭圆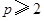 于点
于点 ,
, ,直线
,直线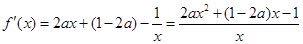 与
与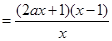 交于点
交于点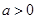 .
.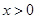 的最大值;
的最大值;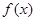 .,
., 两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.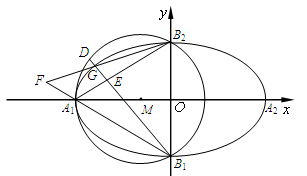
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| FA |
| FB |
| FC |
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
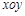 中,已知椭圆的焦点在
中,已知椭圆的焦点在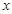 轴上,离心率为
轴上,离心率为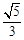 ,且经过点
,且经过点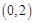 .
.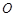 ,设
,设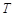 为圆
为圆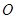 上不在坐标轴上的任意一点,
上不在坐标轴上的任意一点,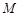 为
为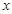 轴上一点,过圆心
轴上一点,过圆心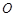 作直线
作直线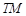 的垂线交椭圆右准线于点
的垂线交椭圆右准线于点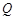 .问:直线
.问:直线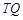 能否与圆
能否与圆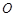 总相切,如果能,求出点
总相切,如果能,求出点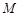 的坐标;如果不能,说明理由.
的坐标;如果不能,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com