
【题目】已知函数f(x)=![]() ,其中a∈R.
,其中a∈R.
(I)当a=1时,求曲线y=f(x)在原点处的切线方程;
(II)求f(x)的极值.
【答案】(I)2x-y=0; (II)见解析.
【解析】试题分析:(1)求出在原点处的导数值,得斜率,即可求出切线方程;
(2)求出导数,讨论单调性得极值.
试题解析:
(I)解:当a=1时,f(x)=![]() ,f '(x)=-2
,f '(x)=-2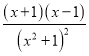 .…………2分
.…………2分
由f '(0)=2,得曲线y=f(x)在原点处的切线方程是2x-y=0.………4分
(II)解:f '(x)=-2![]() . ………6分
. ………6分
①当a=0时,f '(x)=![]() .
.
所以f(x)在(0,+∞)单调递增,(-∞,0)单调递减. ………………7分
当a≠0,f '(x)=-2a .
.
②当a>0时,令f '(x)=0,得x1=-a,x2=![]() ,f(x)与f '(x)的情况如下:
,f(x)与f '(x)的情况如下:
x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
f '(x) | - | 0 | + | 0 | - |
f(x) | ↘ | f(x1) | ↗ | f(x2) | ↘ |
故f(x)的单调减区间是(-∞,-a),(![]() ,+∞);单调增区间是(-a,
,+∞);单调增区间是(-a, ![]() ).
).
f(x)有极小值f(-a)=-1,有极大值f(![]() )=a2 ………10分
)=a2 ………10分
③当a<0时,f(x)与f '(x)的情况如下:
x | (-∞,x2) | x2 | (x2,x1) | x1 | (x1,+∞) |
f '(x) | + | 0 | - | 0 | + |
f(x) | ↗ | f(x2) | ↘ | f(x1) | ↗ |
所以f(x)的单调增区间是(-∞,![]() );单调减区间是(-
);单调减区间是(-![]() ,-a),(-a,+ ∞)。
,-a),(-a,+ ∞)。
f(x)有极小值f(-a)=-1,有极大值f(![]() )=a2 ………………12分
)=a2 ………………12分
综上,a>0时,f(x)在(-∞,-a),(![]() ,+∞)单调递减;在(-a,
,+∞)单调递减;在(-a, ![]() )单调递增.
)单调递增.
a=0时,f(x)在(0,+∞)单调递增,在(-∞,0)单调递减,f(x)有极小值f(-a)=-1,有极大值,f(![]() )=a2;a<0时,f(x)在(-∞,
)=a2;a<0时,f(x)在(-∞, ![]() ),(-a,+∞)单调递增;在(
),(-a,+∞)单调递增;在(![]() ,-a)单调递减,f(x)有极小值f(-a)=-1,有极大值f(
,-a)单调递减,f(x)有极小值f(-a)=-1,有极大值f(![]() )=a2.
)=a2.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全班50人中随机抽取1人,抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上表补充完整(不用写计算过程);
(2)能否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 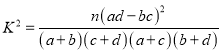 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边的边长分别是a,b,c.已知c=2,C=![]() .
.
(1)若△ABC的面积等于![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B-A)=2sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:①集合![]() 的子集个数有16个;②定义在
的子集个数有16个;②定义在![]() 上的奇函数
上的奇函数![]() 必满足
必满足![]() ;③
;③![]() 既不是奇函数又不是偶函数;④偶函数的图像一定与
既不是奇函数又不是偶函数;④偶函数的图像一定与![]() 轴相交;⑤
轴相交;⑤![]() 在
在![]() 上是减函数。
上是减函数。
其中真命题的序号是 ______________(把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() =(sinx,cosx),
=(sinx,cosx),![]() =(cosφ,sinφ)(|φ|<
=(cosφ,sinφ)(|φ|<![]() ).函数
).函数
f(x)=![]()
![]() 且f(
且f(![]() -x)=f(x).
-x)=f(x).
(Ⅰ)求f(x)的解析式及单调递增区间;
(Ⅱ)将f(x)的图象向右平移![]() 单位得g(x)的图象,若g(x)+1≤ax+cosx在x∈[0,
单位得g(x)的图象,若g(x)+1≤ax+cosx在x∈[0, ![]() ]上恒成立,求实数a的取值范围.
]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前3项和为6,前8项和为-4.
(1)求数列{an}的通项公式;
(2)设bn=(4-an)qn-1 (q≠0,n∈N*),求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .若点
.若点![]() 在椭圆
在椭圆![]() 上,则点
上,则点![]() 称为点
称为点![]() 的一个“椭点”.
的一个“椭点”.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,
, ![]() 两点的“椭点”分别为
两点的“椭点”分别为![]() ,
, ![]() ,以
,以![]() 为直径的圆经过坐标原点,试求
为直径的圆经过坐标原点,试求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com