
(1)若角α的终边和函数y=-|x|的图象重合,试写出角α的集合;
(2)已知角α是第二象限角,试确定2α、![]() 所在的象限;
所在的象限;
(3)若θ角的终边与![]() 角的终边相同,求在[
角的终边相同,求在[![]() ,
,![]() ]内终边与
]内终边与![]() 角的终边相同的角.
角的终边相同的角.
|
思路 求终边相同的角的集合,方法是先求出[0,2π]之间符合条件的角,再根据周期性写出符合条件的角的集合. 解答 (1)由于y=-|x|的图象是三、四象限的平分线,故在 (2)∵α是第二象限角, ∴k· 2k· ∴故2α是第三、第四象限或角的终边在y轴负半轴上. ∵k· 当k=2m(m∈Z)时,m· 当k=2m+1(m∈Z)时,m· ∴ (3)θ=k· 依题意得0≤k· |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:2013-2014学年人教版高考数学文科二轮专题复习提分训练17练习卷(解析版) 题型:解答题
设函数f(θ)= sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为( ,
, ),求f(θ)的值;
),求f(θ)的值;
(2)若点P(x,y)为平面区域Ω:  上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修四1.1任意角和弧度制练习卷(一)(解析版) 题型:填空题
若角α和β的终边满足下列位置关系,试写出α和β的关系式:
(1)重合:________________;
(2)关于x轴对称:________________.
查看答案和解析>>
科目:高中数学 来源:0117 同步题 题型:解答题
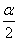 所在的象限;
所在的象限;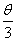 的终边相同的角.
的终边相同的角. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com