Question

已知二次函数f（x）=ax²+bx+c，若f（x）+f（x+1）=2x²-2x+13
（1）求函数f（x）的解析式；
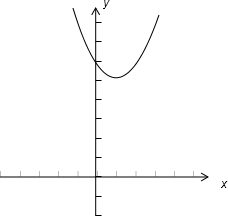
（2）画该函数的图象；
（3）当x∈[t，5]时，求函数f（x）的最大值．

Answer 1

分析：（1）由f（x+1）=a（x+1）²+b（x+1）+c，得到f（x）+f（x+1）=2ax²+（2a+2b）x+a+b+2c=2x²-2x+13，由此求出a，b，c的值，从而得到函数f（x）的解析式．
（2）先求出该函数的对称轴和顶点为坐标，再求出它与y轴的交点坐标，然后结合函数的对称性作出这条开口向上的抛物线．
（3）x∈[t，5]，f（x）=x²-2x+7=（x-1）²+6，当-3≤t≤5时，函数f（x）的最大值为f（5）=f（-3）=9+6+7=22．当t＜-3时，函数f（x）的最大值为f（t）=（t-1）²+6．

解答：解：（1）f（x）+f（x+1）=ax²+bx+c+a（x+1）²+b（x+1）+c=2ax²+（2a+2b）x+a+b+2c
∵f（x）+f（x+1）=2x²-2x+13∴

2a=2 2a+2b=-2 a+b+2c=13

∴

a=1 b=-2 c=7

∴f（x）=x²-2x+7
（2）该函数是对称轴为x=1，顶点为（1，6），与x轴无交点，与y轴交于（0，7），开口向上的抛物线．

（3）∵x∈[t，5]，f（x）=x²-2x+7=（x-1）²+6，
∴当-3≤t≤5时，函数f（x）的最大值为f（5）=f（-3）=9+6+7=22．
当t＜-3时，函数f（x）的最大值为f（t）=（t-1）²+6．
∴f(x)max=

22，-3≤t≤5 (t-1)2+6，t＜-3

．

点评：本题考查二次函数的图象和性质，解题时要认真审题，注意配方法和合理运用和图形结合思想的巧妙运用．