
【题目】如图,在四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点 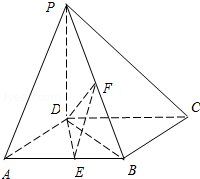
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论;
(3)求DB与平面DEF所成角的正弦值.
【答案】
(1)解:以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系(如图),
设AD=a,则D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)、E(a, ![]() ,0)、F(
,0)、F( ![]() ,
, ![]() ,
, ![]() )、P(0,0,a).
)、P(0,0,a).
∵ ![]() =(﹣
=(﹣ ![]() ,0,
,0, ![]() ),
), ![]() =(0,a,0),
=(0,a,0),
∴ ![]()
![]() =(﹣
=(﹣ ![]() ,0,
,0, ![]() )(0,a,0)=0,
)(0,a,0)=0,
∴ ![]() ⊥
⊥ ![]()
∴EF⊥DC
(2)解:设G(x,0,z),则G∈平面PAD.
![]() =(x﹣
=(x﹣ ![]() ,﹣
,﹣ ![]() ,z﹣
,z﹣ ![]() ),
),
![]()
![]() =(x﹣
=(x﹣ ![]() ,﹣
,﹣ ![]() ,z﹣
,z﹣ ![]() )(a,0,0)=a(x﹣
)(a,0,0)=a(x﹣ ![]() )=0,∴x=
)=0,∴x= ![]() ;
;
![]()
![]() =(x﹣
=(x﹣ ![]() ,﹣
,﹣ ![]() ,z﹣
,z﹣ ![]() )(0,﹣a,a)=
)(0,﹣a,a)= ![]() +a(z﹣
+a(z﹣ ![]() )=0,∴z=0.
)=0,∴z=0.
∴G点坐标为( ![]() ,0,0),即G点为AD的中点
,0,0),即G点为AD的中点
(3)解:设平面DEF的法向量为 ![]() =(x,y,z).
=(x,y,z).
由 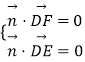 得:
得: 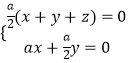
取x=1,则y=﹣2,z=1,
∴ ![]() =(1,﹣2,1).
=(1,﹣2,1).
cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
∴DB与平面DEF所成角的正弦值的大小为 ![]()
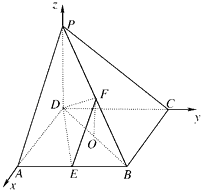
【解析】以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系,设AD=a,可求出各点的坐标;(1)求出EF和CD的方向向量,根据向量垂直的充要条件,可证得 ![]() ⊥
⊥ ![]() ,即EF⊥DC.(2)设G(x,0,z),根据线面垂直的性质,可得
,即EF⊥DC.(2)设G(x,0,z),根据线面垂直的性质,可得 ![]()
![]() =
= ![]()
![]() =0,进而可求出x,z值,得到G点的位置;(3)求出平面DEF的法向量为
=0,进而可求出x,z值,得到G点的位置;(3)求出平面DEF的法向量为 ![]() ,及DB的方向
,及DB的方向 ![]() 的坐标,代入向量夹角公式,可得DB与平面DEF所成角的正弦值
的坐标,代入向量夹角公式,可得DB与平面DEF所成角的正弦值


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知点M(2,2),N(5,-2),点P在x轴上,分别求满足下列条件的点P的坐标.
(1)∠MOP=∠OPN(O是坐标原点).
(2)∠MPN是直角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数 ![]() 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在杨辉三角形中,斜线l的上方从1按箭头所示方向可以构成一个“锯齿形”的数列:1,3,3,4,6,5,10,…,记此数列的前n项之和为Sn , 则S21的值为( ) 
A.66
B.153
C.295
D.361
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx2﹣3x在x=±1处取得极值
(1)求函数f(x)的解析式;
(2)求证:对于区间[﹣1,1]上任意两个自变量的值x1 , x2 , 都有|f(x1)﹣f(x2)|≤4;
(3)若过点A(1,m)(m≠﹣2)可作曲线y=f(x)的三条切线,求实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2﹣4ax+3a2<0(a>0);命题q:实数x满足 ![]()
(1)若a=1,且“p且q”为真,求实数x的取值范围
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c且acosB=4,bsinA=3.
(1)求tanB及边长a的值;
(2)若△ABC的面积S=9,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,MCN是某海湾旅游区的一角,为营造更加优美的旅游环境,旅游区管委会决定建立面积为4 ![]() 平方千米的三角形主题游戏乐园ABC,并在区域CDE建立水上餐厅.已知∠ACB=120°,∠DCE=30°.
平方千米的三角形主题游戏乐园ABC,并在区域CDE建立水上餐厅.已知∠ACB=120°,∠DCE=30°.
(1)设AC=x,AB=y,用x表示y,并求y的最小值;
(2)设∠ACD=θ(θ为锐角),当AB最小时,用θ表示区域CDE的面积S,并求S的最小值.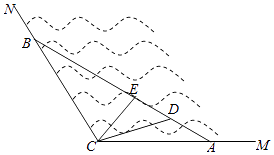
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com