
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
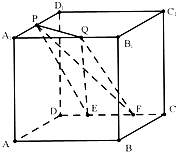 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E、F为CD上两点,且EF的长为定值,则下面四个值中不是定值的是( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E、F为CD上两点,且EF的长为定值,则下面四个值中不是定值的是( )| A、点P到平面QEF的距离 |
| B、直线PQ与平面PEF所成的角 |
| C、三棱锥P-QEF的体积 |
| D、△QEF的面积 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图是某校的校园设施平面图,现用不同的颜色作为各区域的底色,为了便于区分,要求相邻区域不能使用同一种颜色,若有6种不同的颜色可选,则有( )种不同的着色方案.
如图是某校的校园设施平面图,现用不同的颜色作为各区域的底色,为了便于区分,要求相邻区域不能使用同一种颜色,若有6种不同的颜色可选,则有( )种不同的着色方案.| A、480 | B、420 |
| C、360 | D、240 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| a |
| b |
| b |
| c |
| b |
| a |
| c |
| A、①②⑤ | B、② | C、②⑤ | D、①④⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A |
| 2 |
| A、直角三角形 |
| B、锐角三角形 |
| C、钝角三角形 |
| D、等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 拟合曲线 | 直 线 | 指数曲线 | 抛 物 线 | 二次曲线 | ||||||||||
| y与x回归方程 |
|
|
|
| ||||||||||
| 相关指数R2 | 0.746 | 0.996 | 0.902 | 0.002 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图:四边形ABCD是梯形,AB∥CD,AD⊥CD,三角形ADE是等边三角形,且平面ABCD⊥平面ADE,EF∥AB,CD=2AB=2AD=2EF=4,
如图:四边形ABCD是梯形,AB∥CD,AD⊥CD,三角形ADE是等边三角形,且平面ABCD⊥平面ADE,EF∥AB,CD=2AB=2AD=2EF=4,| CG |
| 2 |
| 3 |
| CF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com