
【题目】某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米,该公司准备从两种户型住宅中各拿出12套销售给内部员工,表是这24套住宅每平方米的销售价格:(单位:万元平方米):
房号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.5 |
B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8 | 3.9 | 4.2 | 4.1 | 4.1 | 4.2 | 4.3 | 4.5 |
(1)根据表格数据,完成下列茎叶图,并分别求出A,B两类户型住宅每平方米销售价格的中位数;
A户型 | B户型 | |
2. | ||
3. | ||
4. |
(2)该公司决定对上述24套住房通过抽签方式销售,购房者根据自己的需求只能在其中一种户型中通过抽签方式随机获取房号,每位购房者只有一次抽签机会,小明是第一位抽签的员工,经测算其购买能力最多为320万元,抽签后所抽得住房价格在其购买能力范围内则确定购买,否则,将放弃此次购房资格,为了使其购房成功的概率更大,他应该选择哪一种户型抽签?
【答案】(1)茎叶图见解析. ![]() 户型销售价格的中位数是
户型销售价格的中位数是![]() ,
,![]() 户型销售价格的中位数是
户型销售价格的中位数是![]() (2) 小明应该选择
(2) 小明应该选择![]() 户型抽签.
户型抽签.
【解析】
(1)由表格数据,能作出茎叶图,并能求出![]() 类户型住宅每平方米销售价格的中位数.
类户型住宅每平方米销售价格的中位数.
(2)若选择![]() 户型抽签,求出成功购房的概率;若选择
户型抽签,求出成功购房的概率;若选择![]() 户型抽签,求出成功购房的概率.由此得到该员工选择购买
户型抽签,求出成功购房的概率.由此得到该员工选择购买![]() 户型住房的概率较大.
户型住房的概率较大.
(1)由表格数据,作出茎叶图:
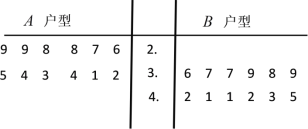
![]() 户型销售价格的中位数是
户型销售价格的中位数是![]()
![]() 户型销售价格的中位数是
户型销售价格的中位数是![]()
(2)小明购买能力最多为320万元.
若选择![]() 户型抽签,则每平方米均价不得高于3.2万元,
户型抽签,则每平方米均价不得高于3.2万元,
有能力购买其中的8套住房,
∴成功购房的概率是![]()
若选择![]() 户型抽签,每平方米均价不得高于4.0万元,有能力购买其中的6套住房,
户型抽签,每平方米均价不得高于4.0万元,有能力购买其中的6套住房,
成功购房的概率是![]()
所以小明选择购买![]() 户型成功的概率更大. 他应该选择
户型成功的概率更大. 他应该选择![]() 户型抽签.
户型抽签.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】为了解某市的交通状况,现对其6条道路进行评估,得分分别为:5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如表
评估的平均得分 | (0,6] | (6,8] | (8,10] |
全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级.
(2)用简单随机抽样方法从这6条道路中抽取2条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,
(1)求![]() 的解析式;
的解析式;
(2)关于![]() 的不等式
的不等式![]() 的解集为一切实数,求实数
的解集为一切实数,求实数![]() 的取值范围;
的取值范围;
(3)关于![]() 的不等式
的不等式![]() 的解集中的正整数解恰有
的解集中的正整数解恰有![]() 个,求实数
个,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把边长为a的等边三角形铁皮剪去三个相同的四边形(如图阴影部分)后,用剩余部分做成一个无盖的正三棱柱形容器(不计接缝),设容器的高为x,容积为![]() .
.
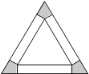
(1)写出函数![]() 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
(2)求当x为多少时,容器的容积最大?并求出最大容积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com