已知函数f(x)=logax,(a>0且a≠1).
(1)若g(x)=f(|x|),当a>1时,解不等式g(1)<g(lgx);
(2)若函数h(x)=|f(x-a)|-1,讨论h(x)在区间[2,4]上的最小值.
解:(1)g(x)=log
a|x|是偶函数
当x>0时,
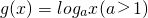
是增函数,当x<0时,g(x)=log
a(-x)(a>1)是减函数,
∵g(1)<g(lgx),∴g(1)<g(|lgx|),
∴1<|lgx|,
∴lgx<-1或lgx>1
∴0<x<0.1或x>10;
∴不等式的解集为:{x|0<x<0.1或x>10}
(2)h(x)=|f(x-a)|-1=|log
a(x-a)|-1
∵x-a>0,x∈[2,4],∴0<a<4且a≠1
若x=a+1时,log
a(x-a)=0
①当2<a+1≤4,则1<a≤3,∴x=a+1时,h(x)
min=h(a+1)=-1.
②当a+1<2,则0<a<1,在x∈[2,4]时,h(x)为增函数,
∴x=2时,h(x)
min=h(2)=-log
a(2-a)-1.
③当a+1>4,则3<a<4,在x∈[2,4]时,h(x)为减函数.
∴x=4时,h(x)
min=h(4)=-log
a(4-a)-1.
∴h(x)
min=

.
分析:(1)g(x)=log
a|x|是偶函数,当x>0时,
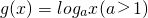
是增函数,当x<0时,g(x)=log
a(-x)(a>1)是减函数,不等式g(1)<g(lgx),等价于g(1)<g(|lgx|),利用单调性,即可求得不等式的解集;
(2)h(x)=|f(x-a)|-1=|log
a(x-a)|-1,根据x-a>0,x∈[2,4],可得0<a<4且a≠1,由于x=a+1时,log
a(x-a)=0,故需要分类讨论,从而确定h(x)在区间[2,4]上的最小值.
点评:本题是函数的单调性与奇偶性的综合,考查解不等式,考查利用单调性求函数的最值,考查分类讨论的数学思想.

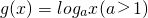 是增函数,当x<0时,g(x)=loga(-x)(a>1)是减函数,
是增函数,当x<0时,g(x)=loga(-x)(a>1)是减函数, .
.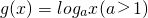 是增函数,当x<0时,g(x)=loga(-x)(a>1)是减函数,不等式g(1)<g(lgx),等价于g(1)<g(|lgx|),利用单调性,即可求得不等式的解集;
是增函数,当x<0时,g(x)=loga(-x)(a>1)是减函数,不等式g(1)<g(lgx),等价于g(1)<g(|lgx|),利用单调性,即可求得不等式的解集;
