
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
【答案】
(1)
证明:取BC中点E,连结EN,EM,
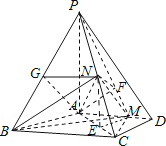
∵N为PC的中点,∴NE是△PBC的中位线,
∴NE∥PB,
又∵AD∥BC,∴BE∥AD,
∵AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,
∴BE= ![]() BC=AM=2,
BC=AM=2,
∴四边形ABEM是平行四边形,
∴EM∥AB,∴平面NEM∥平面PAB,
∵MN平面NEM,∴MN∥平面PAB
(2)
解:在△AMC中,由AM=2,AC=3,cos∠MAC= ![]() ,得CM2=AC2+AM2﹣2ACAMcos∠MAC=9+4-
,得CM2=AC2+AM2﹣2ACAMcos∠MAC=9+4- ![]() =5.
=5.
∴AM2+MC2=AC2,则AM⊥MC,
∵PA⊥底面ABCD,PA平面PAD,
∴平面ABCD⊥平面PAD,且平面ABCD∩平面PAD=AD,
∴CM⊥平面PAD,则平面PNM⊥平面PAD.
在平面PAD内,过A作AF⊥PM,交PM于F,连接NF,则∠ANF为直线AN与平面PMN所成角.
在Rt△PAC中,由N是PC的中点,得AN= ![]() ,
,
在Rt△PAM中,由PAAM=PMAF,得AF= ![]() ,
,
∴ 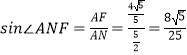 .
.
∴直线AN与平面PMN所成角的正弦值为 ![]()
【解析】(1)法一、取PB中点G,连接AG,NG,由三角形的中位线定理可得NG∥BC,且NG= ![]() BC,再由已知得AM∥BC,且AM=
BC,再由已知得AM∥BC,且AM= ![]() BC,得到NG∥AM,且NG=AM,说明四边形AMNG为平行四边形,可得NM∥AG,由线面平行的判定得到MN∥平面PAB;
BC,得到NG∥AM,且NG=AM,说明四边形AMNG为平行四边形,可得NM∥AG,由线面平行的判定得到MN∥平面PAB;
法二、证明MN∥平面PAB,转化为证明平面NEM∥平面PAB,在△PAC中,过N作NE⊥AC,垂足为E,连接ME,由已知PA⊥底面ABCD,可得PA∥NE,通过求解直角三角形得到ME∥AB,由面面平行的判定可得平面NEM∥平面PAB,则结论得证;
(2)连接CM,证得CM⊥AD,进一步得到平面PNM⊥平面PAD,在平面PAD内,过A作AF⊥PM,交PM于F,连接NF,则∠ANF为直线AN与平面PMN所成角.然后求解直角三角形可得直线AN与平面PMN所成角的正弦值.本题考查直线与平面平行的判定,考查直线与平面所成角的求法,考查数学转化思想方法,考查了空间想象能力和计算能力,是中档题.


科目:高中数学 来源: 题型:
【题目】
如图,四棱锥P -ABCD的底面是矩形,侧面PAD是正三角形,
且侧面PAD⊥底面ABCD,E 为侧棱PD的中点。
(1)求证:PB//平面EAC;
(2)求证:AE⊥平面PCD;
(3)当![]() 为何值时,PB⊥AC ?
为何值时,PB⊥AC ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() R,函数
R,函数 ![]() =
= ![]() .
.
(1)当 ![]() 时,解不等式
时,解不等式 ![]() >1;
>1;
(2)若关于 ![]() 的方程
的方程 ![]() +
+ ![]() =0的解集中恰有一个元素,求
=0的解集中恰有一个元素,求 ![]() 的值;
的值;
(3)设 ![]() >0,若对任意
>0,若对任意 ![]()
![]() ,函数
,函数 ![]() 在区间
在区间 ![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岸![]() 处发现北偏东
处发现北偏东![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处有一艘走私船,在
处有一艘走私船,在![]() 处北偏西
处北偏西![]() 方向,距
方向,距![]() 处
处![]() 海里的
海里的![]() 处的我方辑私船奉命以
处的我方辑私船奉命以![]() 海里/小时的速度追截走私船,此时走私船正以
海里/小时的速度追截走私船,此时走私船正以![]() 海里/小时的速度,以
海里/小时的速度,以![]() 处向北偏东
处向北偏东![]() 方向逃窜.问:辑私船沿什么方向行驶才能最快截获走私船?并求出所需时间.
方向逃窜.问:辑私船沿什么方向行驶才能最快截获走私船?并求出所需时间.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个类比中,正确的个数为
(1)若一个偶函数在R上可导,则该函数的导函数为奇函数。将此结论类比到奇函数的结论为:若一个奇函数在R上可导,则该函数的导函数为偶函数。
(2)若双曲线的焦距是实轴长的2倍,则此双曲线的离心率为2.将此结论类比到椭圆的结论为:若椭圆的焦距是实轴长的一半,则此椭圆的离心率为![]() .
.
(3)若一个等差数列的前3项和为1,则该数列的第2项为![]() .将此结论类比到等比数列的结论为:若一个等比数列的前3项积为1,则该数列的第2项为1
.将此结论类比到等比数列的结论为:若一个等比数列的前3项积为1,则该数列的第2项为1
(4)在平面上,若两个正三角形的边长比为1:2,则它们的面积比为1:4.将此结论类比到空间中的结论为:在空间中,若两个正四面体的棱长比为1:2,则它们的体积比为1:8.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣ ![]() ,g(x)=x2﹣2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),求实数a的取值范围.
,g(x)=x2﹣2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c.设向量 ![]() =(a,c),
=(a,c), ![]() =(cosC,cosA).
=(cosC,cosA).
(1)若 ![]() ,c=
,c= ![]() a,求角A;
a,求角A;
(2)若 ![]() =3bsinB,cosA=
=3bsinB,cosA= ![]() ,求cosC的值.
,求cosC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com