【题目】点
是抛物线
：
的焦点，动直线
过点且与抛物线相交于
，
两点.当直线变化时，
的最小值为4.
（1）求抛物线的标准方程；
（2）过点，分别作抛物线的切线
，
，与相交于点
，，与
轴分别交于点
，
，求证：
与
的面积之比为定值（
为坐标原点）.
【答案】（1）
（2）见解析
【解析】
（1）证明直线的斜率为
时不合题意，当直线的斜率不为时，设直线
的方程为
，与抛物线方程联立，消元，用根与系数的关系得出
两点横坐标的关系，利用焦点弦长计算公式求
，利用二次函数的性质得出
的值，进而得出抛物线的方程；
（2）用两点的坐标表示直线
，
的方程，再求点
的横坐标，根据三角形的面积公式求比值，即可得出结论.
（1）设
，由已知得当直线的斜率为时，与
有且只有一个交点，此时不合题意
设直线的方程为
联立直线与抛物线的方程，并消去
，得
，则
显然当
时，
取得最小值，则
故抛物线的标准方程为
（2）证明：不妨设
易得切线
，将
代入，整理得
进而可知
同理可得
联立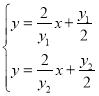
，消去
，整理得到
即点的横坐标为
故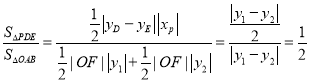
故
与
的面积之比为定值
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，可见部分如下：
试根据图表中的信息解答下列问题：
(1)求全班的学生人数及分数在[70,80)之间的频数；
(2)为快速了解学生的答题情况，老师按分层抽样的方法从位于[70,80)，[80,90)和[90,100]分数段的试卷中抽取8份进行分析，再从中任选3人进行交流，求交流的学生中，成绩位于[70,80)分数段的人数X的分布列和数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，曲线
的参数方程为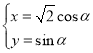
（
为参数）．在以
为极点，
轴正半轴为极轴的极坐标系中，直线
的极坐标方程为
．
（Ⅰ）求曲线的普通方程和直线的直角坐标方程；
（Ⅱ）设点
，若直线与曲线交于
，
两点，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校从高一年级学生中随机抽取60名学生，将期中考试的物理成绩（均为整数）分成六段：
，
，
，…，
后得到如图频率分布直方图.
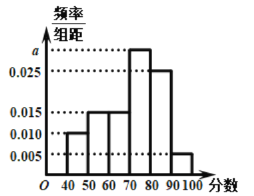
（1）根据频率分布直方图，估计众数和中位数；
（2）用分层抽样的方法从
的学生中抽取一个容量为5的样本，从这五人中任选两人参加补考，求这两人的分数至少一人落在的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的图像与
轴的相邻两交点的坐标分别为
，
，且当
时，
有最小值.
（1）求函数的解析式及单调递减区间；
（2）将的图像向右平移
个单位，再将所得图像的横坐标伸长为原来的
倍（纵坐标不变），得到函数
的图像，若关于的方程
在区间
上有两个解，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知：在平面四边形ABCD中，
，
，
，
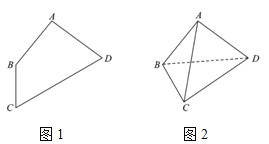
（如图1），若将
沿对角线BD折叠，使
（如图2）.请在图2中解答下列问题.
（1）证明：
；
（2）求三棱锥
的高.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】把一个圆分成n（n≥2）个扇形，依次记为
，每一扇形都可用红、白、蓝三种不同颜色的任一种涂色，要求相邻的扇形的颜色互不相同，问有多少种涂色法？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}满足
an+1
an=0(n∈N*)，且
，
，
成等差数列．
（1）求数列{an}的通项公式;
（2）令bn=
(n∈N*)，求数列{bn}的前n项和为
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
