
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,其图象上存在一点
,其图象上存在一点![]() ,使此处切线的斜率
,使此处切线的斜率![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,方程
时,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3)![]()
【解析】试题分析:(1)依题意确定![]() 的定义域,对
的定义域,对![]() 求导,求出函数的单调性,即可求出函数
求导,求出函数的单调性,即可求出函数![]() 的最大值;(2)表示出
的最大值;(2)表示出![]() ,根据其图象上存在一点
,根据其图象上存在一点![]() ,使此处切线的斜率
,使此处切线的斜率![]() 可得
可得![]() ,在
,在![]() 上有解,即可求出实数
上有解,即可求出实数![]() 的取值范围;(3)由
的取值范围;(3)由![]() ,方程
,方程![]() 有唯一实数解,构造函数
有唯一实数解,构造函数![]() ,求出
,求出![]() 的单调性,即可求出正数
的单调性,即可求出正数![]() 的值.
的值.
试题解析:(1)依题意, ![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时, ![]() ,
, ![]()
由![]() ,得
,得![]() ,解得
,解得![]()
由![]() ,得
,得![]() ,解得
,解得![]() 或
或![]()
∵![]() ,∴
,∴![]() 在
在![]() 单调递増,在
单调递増,在![]() 单调递减;所以
单调递减;所以![]() 的极大值为
的极大值为![]() ,此即为最大值
,此即为最大值
(2)![]() ,则有
,则有![]() ,在
,在![]() 上有解,
上有解,
∴![]() ,
, ![]() ,∵
,∵![]() ,所以当
,所以当![]() 时,
时, ![]()
取得最小值![]() ,∴
,∴![]()
(3)由![]() 得
得![]() ,令
,令![]() ,
, 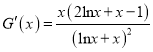
令![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,
,
∴在![]() ,即
,即![]() ,在
,在![]() ,即
,即![]() ,
,
∴![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递増,∴
单调递増,∴![]() 极小值
极小值![]() ,令
,令![]() ,即
,即![]() 时方程
时方程![]() 有唯一实数解.
有唯一实数解.


科目:高中数学 来源: 题型:
【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间[20,50]岁之间,对区间[20,50]岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 人数(单位:人) |
第一组 | [20,25) | 2 |
第二组 | [25,30) | a |
第三组 | [30,35) | 5 |
第四组 | [35,40) | 4 |
第五组 | [40,45) | 3 |
第六组 | [45,50] | 2 |

(Ⅰ)求a的值并画出频率分布直方图;
(Ⅱ)在统计表的第五与第六组的5人中,随机选取2人,求这2人的年龄都小于45岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海轮以每小时30海里的速度航行,在点![]() 测得海面上油井
测得海面上油井![]() 在南偏东
在南偏东![]() ,海轮向北航行40分钟后到达点
,海轮向北航行40分钟后到达点![]() ,测得油井
,测得油井![]() 在南偏东
在南偏东![]() ,海轮改为北偏东
,海轮改为北偏东![]() 的航向再行驶80分钟到达点
的航向再行驶80分钟到达点![]() ,则
,则![]() 两点的距离为(单位:海里)
两点的距离为(单位:海里)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大西洋鲑鱼每年都要逆流而上,游回产地产卵,经研究发现鲑鱼的游速可以表示为函数y=![]() log3(
log3(![]() ),单位是m/s,θ是表示鱼的耗氧量的单位数.
),单位是m/s,θ是表示鱼的耗氧量的单位数.
(1)当一条鲑鱼的耗氧量是900个单位时,它的游速是多少?
(2)计算一条鱼静止时耗氧量的单位数。
(3)某条鲑鱼想把游速提高1 m/s,那么它的耗氧量的单位数是原来的多少倍?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)对任意的m,n∈R都有f(m+n)=f(m)+f(n)-1,并且x>0时,恒有f(x)>1.
(1)求证:f(x)在R上是增函数;
(2)若f(3)=4,解不等式f(a2+a-5)<2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位建造一间地面面积为12![]() 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度![]() 不得超过
不得超过![]() 米,房屋正面的造价为400元/
米,房屋正面的造价为400元/![]() ,房屋侧面的造价为150元/
,房屋侧面的造价为150元/![]() ,屋顶和地面的造价费用合计为5800元,如果墙高为3
,屋顶和地面的造价费用合计为5800元,如果墙高为3![]() ,且不计房屋背面的费用.
,且不计房屋背面的费用.
(1)把房屋总价![]() 表示成
表示成![]() 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(2)当侧面的长度为多少时,总造价最低?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于在区间![]() 上有意义的函数
上有意义的函数![]() ,满足对任意的
,满足对任意的![]() ,
,![]() ,有
,有![]() 恒成立,厄称
恒成立,厄称![]() 在
在![]() 上是“友好”的,否则就称
上是“友好”的,否则就称![]() 在
在![]() 上是“不友好”的,现有函数
上是“不友好”的,现有函数![]() .
.
(1)若函数![]() 在区间
在区间![]() (
(![]() )上是“友好”的,求实数
)上是“友好”的,求实数![]() 的取值范围;
的取值范围;
(2)若关于![]() 的方程
的方程![]() 的解集中有且只有一个元素,求实数
的解集中有且只有一个元素,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com