
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥底面ABCD,PD⊥AD,PD=AD,E为棱PC的中点

(I)证明:平面PBC⊥平面PCD;
(II)求直线DE与平面PAC所成角的正弦值;
(III)若F为AD的中点,在棱PB上是否存在点M,使得FM⊥BD?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(Ⅰ)见解析(II)![]() (III)存在,
(III)存在,![]() =
=![]()
【解析】
(I)由面面垂直的性质定理得PD⊥底面ABCD,从而可得BC⊥平面PCD,然后可证得面面垂直;
(II)以![]() 为
为![]() 轴建立空间直角坐标系,写出各点坐标,求出平面的法向量和直线的方向向量,平面的法向量和直线的方向向量的余弦的绝对值等于直线与平面所成角的正弦;
轴建立空间直角坐标系,写出各点坐标,求出平面的法向量和直线的方向向量,平面的法向量和直线的方向向量的余弦的绝对值等于直线与平面所成角的正弦;
(III)设![]() =λ
=λ![]() (0≤λ≤1),由
(0≤λ≤1),由![]() 求得
求得![]() 即可.
即可.
(I)∵平面PAD⊥底面ABCD,又PD⊥AD,
∴PD⊥底面ABCD
∴PD⊥BC
又∵底面ABCD为正方形,BC⊥CD
∴BC⊥平面PCD
∴平面PBC⊥平面PCD,
(II)由(I)知,PD⊥底面ABCD,AD⊥CD
如图以点D为原点建立空间直角坐标系
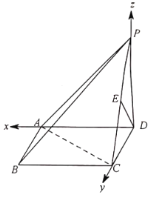
不妨设PD=AD=2,可得D(0,0,0),A(2,0,0,),C(0,2,0),P(0,0,2),
由E为棱PC的中点,得E(0,1,1),![]()
向量![]() =(-2,2,0),
=(-2,2,0),![]() =(2,0,-2),设
=(2,0,-2),设![]() =(x,y,z)为平面PAC的法向量,则
=(x,y,z)为平面PAC的法向量,则
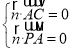 ,即
,即![]()
不妨令x=1,可得![]() =(1,1,1)为平面PAC的一个法向量
=(1,1,1)为平面PAC的一个法向量
设直线DE与平面PAC所成角为θ
所以sinθ=![]() =
=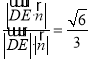
所以,直线DE与平面PAC所成角的正弦值为![]()
(III)向量![]() =(-2,-2,2),
=(-2,-2,2),![]() =(2,2,0),
=(2,2,0),![]() =(1,2,0)
=(1,2,0)
由点M在棱PB上,设![]() =λ
=λ![]() (0≤λ≤1)
(0≤λ≤1)
故![]() =
=![]() +
+![]() =(1-2λ,2-2λ,2λ)
=(1-2λ,2-2λ,2λ)
由FM⊥DB,得![]() ·
·![]() =0
=0
因此(1-2λ)×2+(2-2λ)×2=0
解得λ=![]() ,所以
,所以![]() =
=![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】根据下图给出的2000年至2016年我国实际利用外资情况,以下结论正确的是

A. 2000年以来我国实际利用外资规模与年份负相关
B. 2010年以来我国实际利用外资规模逐年增加
C. 2008年我国实际利用外资同比增速最大
D. 2010年以来我国实际利用外资同比增速最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有限集![]() . 如果
. 如果![]() 中元素
中元素![]() 满足
满足![]() ,就称
,就称![]() 为“复活集”,给出下列结论:
为“复活集”,给出下列结论:
①集合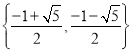 是“复活集”;
是“复活集”;
②若![]() ,且
,且![]() 是“复活集”,则
是“复活集”,则![]() ;
;
③若![]() ,则
,则![]() 不可能是“复活集”;
不可能是“复活集”;
④若![]() ,则“复活集”
,则“复活集”![]() 有且只有一个,且
有且只有一个,且![]() .
.
其中正确的结论是____________.(填上你认为所有正确的结论序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com