练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    .(20分) 已知中心在原点的双曲线C的一个焦点是，一条渐近线的方程是．

    （1）求双曲线C的方程；w.w.w.k.s.5.u.c.o.m    

    （2）若以为斜率的直线与双曲线C相交于两个不同的点M，N，且线段MN的垂直平分线与两坐标轴围成的三角形的面积为，求的取值范围．

    （1）解析：设双曲线的方程为（）．由题设得

    ，解得，所以双曲线方程为．---------------------（5分）

    （2）解：设直线的方程为（）．点，的坐标满足方程组 w.w.w.k.s.5.u.c.o.m    

    将①式代入②式，得，w.w.w.k.s.5 u.c.o.m整理得．

    此方程有两个不等实根，于是，且．整理得③由根与系数的关系可知线段的中点坐标满足

    ，．------------------------（10分）

    从而线段的垂直平分线方程为．

    此直线与轴，轴的交点坐标分别为，．由题设可得，．解得

    或．所以的取值范围是----（20分）

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    甲和乙参加智力答题活动，活动规则：①答题过程中，若答对则继续答题；若答错则停止答题；②每人最多答3个题；③答对第一题得10分，第二题得20分，第三题得30分，答错得0分．已知甲答对每个题的概率为
    3
    4
    ，乙答对每个题的概率为
    1
    3
    ．
    （Ⅰ）求甲恰好得30分的概率；
    （Ⅱ）设乙的得分为ξ，求ξ的分布列和数学期望；
    （Ⅲ）求甲恰好比乙多30分的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网已知某职业技能培训班学生的项目A与项目B成绩抽样统计表如下，抽出学生n人，成绩只有3、4、5三种分值，设x，y分别表示项目A与项目B成绩．例如：表中项目A成绩为5分的共7+9+4=20人．已知x=4且y=5的概率是0.2．
    （1）求n；
    （2）若在该样本中，再按项目B的成绩分层抽样抽出20名学生，则y=3的学生中应抽多少人？
    （3）已知a≥9，b≥2，项目B为3分的学生中，求项目A得3分的人数比得4分人数多的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某电脑生产企业根据市场调查分析，决定调整产品生产方案，准备每周（按40个工作时计算）生产联想、方正、海尔三种电脑共120台，且海尔至少生产20台．已知生产这些电脑产品每台所需工时和每台产值如下表：
    电脑名称 联想 方正 海尔
    工时
    1
    2
    1
    3
    1
    4
    产值（千元） 4 3 2
    （Ⅰ）若生产联想与方正分别是x台、y台，试写出x、y满足的条件，并在给出的直角坐标系中画出相应的平面区域．
    （Ⅱ）每周生产联想、方正、海尔各多少台，才能使产值最高，最高产值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2008•成都三模）某中学开展“创建文明城市知识竞赛”活动，竞赛题由20道选择题构成，每道选择题有4个选项，其中有且只有1个选项是正确的，要求学生在规定时间内通过笔试完成，且每道题必须选出一个选项（不得多选和不选），每道题选择正确得6分，选择错误得0分．已知学生甲对任一道题选择正确的概率是
    34
    ；学生乙由于未作准备，因此只能从每道题的4个选项中随机地选择1个．
    （1）比较甲得66分的概率与乙得54分的概率的大小；
    （2）就前两道题而言，求甲、乙两人得分之和不得低于18分的概率．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年北京四中高三第一学期开学测试数学理卷 题型：解答题

    （本小题满分13分）

    　　甲和乙参加智力答题活动，活动规则：①答题过程中，若答对则继续答题；若答错则停止答题；②每人最多答3个题；③答对第一题得10分，第二题得20分，第三题得30分，答错得0分。已知甲答对每个题的概率为，乙答对每个题的概率为。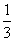

    　　（1）求甲恰好得30分的概率；

    　　（2）设乙的得分为，求的分布列和数学期望；

    　　（3）求甲恰好比乙多30分的概率.

     

    查看答案和解析>>

    同步练习册答案