
| A. | -$\frac{\sqrt{1-{t}^{2}}}{t}$ | B. | $\frac{\sqrt{1-{t}^{2}}}{t}$ | C. | $\frac{\sqrt{1+{t}^{2}}}{t}$ | D. | -$\frac{\sqrt{1+{t}^{2}}}{t}$ |
分析 由已知利用诱导公式可求cos80°=-t,由同角三角函数基本关系式可得sin80°=$\sqrt{1-{t}^{2}}$,tan80$°=\frac{sin80°}{cos80°}$=-$\frac{\sqrt{1-{t}^{2}}}{t}$,由诱导公式化简所求后即可得解.
解答 解:∵cos(-820°)=cos(2×360°+90°+10°)=-cos80°=t,
∴cos80°=-t,(t<0),可得:sin80°=$\sqrt{1-{t}^{2}}$,tan80$°=\frac{sin80°}{cos80°}$=-$\frac{\sqrt{1-{t}^{2}}}{t}$,
∴tan(-440°)=-tan(360°+80°)=-tan80°=$\frac{\sqrt{1-{t}^{2}}}{t}$.
故选:B.
点评 本题主要考查了诱导公式可,同角三角函数基本关系式的综合应用,考查了计算能力,属于基础题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1或2 | B. | -8或-1 | C. | -8或2 | D. | -8,-1或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 周一 | 无雨 | 无雨 | 有雨 | 有雨 |
| 周二 | 无雨 | 有雨 | 无雨 | 有雨 |
| 收益 | 20万 | 15万 | 10万 | 7.5万 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
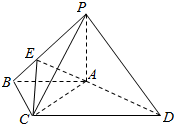 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=∠CAD=90°,点E在棱PB上,且PE=2EB,PA=AB=BC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=∠CAD=90°,点E在棱PB上,且PE=2EB,PA=AB=BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com