
分析 设m>0,n>0,m≠n,设原来价格为1,有三种降价方案:方案①:先降m%,再降n%,价格变为:(1-m%)(1-n%);方案②:先降$\frac{m+n}{2}%$,再降$\frac{m+n}{2}%$,共降了:(1-$\frac{m+n}{2}%$)(1-$\frac{m+n}{2}%$).方案③:一次性降价1-(m+n)%.通过作差比较即可得出大小关系.
解答 解:设m>0,n>0,m≠n,设原来价格为1,有三种降价方案:
方案①:先降m%,再降n%,价格变为:(1-m%)(1-n%);
方案②:先降$\frac{m+n}{2}%$,再降$\frac{m+n}{2}%$,共降了:(1-$\frac{m+n}{2}%$)(1-$\frac{m+n}{2}%$).
方案③:一次性降价1-(m+n)%.
∵(1-$\frac{m+n}{2}%$)(1-$\frac{m+n}{2}%$)-(1-m%)(1-n%)=$(\frac{m+n}{2}%)^{2}$-(mn)%=$\frac{[(m-n)%]^{2}}{4}$>0,
(1-$\frac{m+n}{2}%$)(1-$\frac{m+n}{2}%$)-[1-(m+n)%]=$(\frac{m+n}{2}%)^{2}$>0.
∴降价幅度最小的方案是②.
故答案为:②.
点评 本题考查了数列的应用、作差法,考查了推理能力与计算能力,属于中档题.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.3 | C. | 0.7 | D. | 与σ的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,PA⊥AB,CD⊥AD,BC=CD=$\frac{1}{2}$AD,E为AD的中点.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AD∥BC,PA⊥AB,CD⊥AD,BC=CD=$\frac{1}{2}$AD,E为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
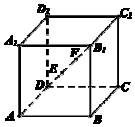 如图,在正方体ABCD-A1B1C1D1中,AB=3$\sqrt{3}$,点E,F在线段DB1上,且DE=EF=FB1,点M是正方体表面上的一动点,点P,Q是空间两动点,若$\frac{|PE|}{|PF|}$=$\frac{|QE|}{|QF|}$=2且|PQ|=4,则$\overrightarrow{MP}$•$\overrightarrow{MQ}$的最小值为-$\frac{8}{3}$.
如图,在正方体ABCD-A1B1C1D1中,AB=3$\sqrt{3}$,点E,F在线段DB1上,且DE=EF=FB1,点M是正方体表面上的一动点,点P,Q是空间两动点,若$\frac{|PE|}{|PF|}$=$\frac{|QE|}{|QF|}$=2且|PQ|=4,则$\overrightarrow{MP}$•$\overrightarrow{MQ}$的最小值为-$\frac{8}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com