�⣺��1������ã�

=��x��y��.

=��4��y
0��.

=��4-x
1��y
0-y
1����
��
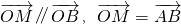
��
��
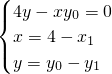
?
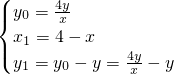
��2���ߵ�A��x
1��y
1����Բ��x-2��
2+y
2=4���˶���
�ࣨx
1-2��
2+y
12=4?
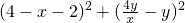
=4��
��
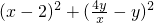
=4��
�ද��M�Ĺ켣����Ϊ
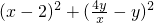
=4��
�����ã�x-4����
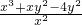
��=0?x=4��x
3+xy
2-4y
2=0��
��Ϊ��x=4ʱ��A������Ϊ��0��0����������������ì�ܣ�
�ද��M�Ĺ켣�����ǣ�x
3+xy
2-4y
2=0��
��3���ٹ���X��Գƣ�
�������еģ�x��y�����ɣ�x��-y����������ʽ���䣬�ʹ���X��Գƣ�
�ڶ���Ϊ��0��0����
�ڷ����У���y=0��x=0�������ߵĶ�������Ϊ��0��0����
��ͼ��Χ�ǣ�0��x��4��y��R��
��
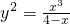
��0��0��x��4��y��R��
��ֱ��x=4�����ߵĽ����ߣ�
��0��x��4��
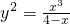
����x��4ʱ��y���ޣ�
��ֱ��x=4�����ߵĽ����ߣ�
��������1���������

=��x��y��.

=��4��y
0��.

=��4-x
1��y
0-y
1�������������á�
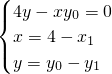
���ɽ��ʾy
0��x
1��y
1��
��2��������ĵ�A���������Բ��x-2��
2+y
2=4�У����������������M�Ĺ켣����F��x��y��=0��
��3�����Ƚ������еģ�x��y�����ɣ�x��-y����������ʽ���䣬�ù���X��Գƣ�
����y=0��x=0�������ߵĶ�������Ϊ��0��0����
�۰ѹ켣����F��x��y��=0�����
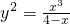
����Ϊƽ�������ڵ���0��0��x��4��y��R��
��0��x��4��
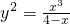
����x��4ʱ��y���ޣ��ɵ�ֱ��x=4�����ߵĽ����ߣ�
������������Ҫ���������ڼ����е�Ӧ���Լ��켣���̵���������ѵ����ڶԹ켣���̵�����������һ�����⣮

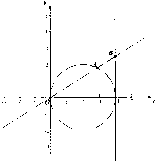 ��֪��A��x1��y1����Բ��x-2��2+y2=4���˶�����A���루0��0���غϣ���B��4��y0����ֱ��x=4���˶�������M��x��y������
��֪��A��x1��y1����Բ��x-2��2+y2=4���˶�����A���루0��0���غϣ���B��4��y0����ֱ��x=4���˶�������M��x��y������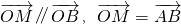 ������M�Ĺ켣C�ķ���ΪF��x��y��=0��
������M�Ĺ켣C�ķ���ΪF��x��y��=0�� =��x��y��.
=��x��y��. =��4��y0��.
=��4��y0��. =��4-x1��y0-y1����
=��4-x1��y0-y1����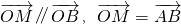 ��
��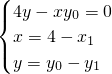 ?
?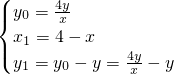
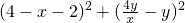 =4��
=4��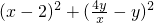 =4��
=4��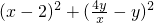 =4��
=4��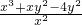 ��=0?x=4��x3+xy2-4y2=0��
��=0?x=4��x3+xy2-4y2=0��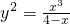 ��0��0��x��4��y��R��
��0��0��x��4��y��R��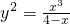 ����x��4ʱ��y���ޣ�
����x��4ʱ��y���ޣ� =��x��y��.
=��x��y��. =��4��y0��.
=��4��y0��. =��4-x1��y0-y1�������������á�
=��4-x1��y0-y1�������������á�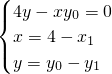 ���ɽ��ʾy0��x1��y1��
���ɽ��ʾy0��x1��y1��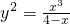 ����Ϊƽ�������ڵ���0��0��x��4��y��R��
����Ϊƽ�������ڵ���0��0��x��4��y��R��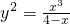 ����x��4ʱ��y���ޣ��ɵ�ֱ��x=4�����ߵĽ����ߣ�
����x��4ʱ��y���ޣ��ɵ�ֱ��x=4�����ߵĽ����ߣ�

 ����ѧ����ϵ�д�
����ѧ����ϵ�д�