
【题目】若无穷数列![]() 满足:
满足:![]() ,当
,当![]() ,
,![]() 时.
时.
![]() 其中
其中![]() 表示
表示![]() ,
,![]() ,
,![]() ,
,![]() 中的最大项
中的最大项![]() ,有以下结论:
,有以下结论:
![]() 若数列
若数列![]() 是常数列,则
是常数列,则![]()
![]() 若数列
若数列![]() 是公差
是公差![]() 的等差数列,则
的等差数列,则![]() ;
;
![]() 若数列
若数列![]() 是公比为q的等比数列,则
是公比为q的等比数列,则![]()
则其中正确的结论是______![]() 写出所有正确结论的序号
写出所有正确结论的序号![]()
科目:高中数学 来源: 题型:
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从某市移动支付用户中随机抽取100人进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
总计 | 15 | 12 | 13 | 7 | 8 | 45 |
(1)把每周使用移动支付6次及以上的用户称为“移动支付达人”,按分层抽样的方法,从参与调查的“移动支付达人”中,随机抽取6人,求抽取的6人中,男、女用户各多少人;
(2)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,根据表格中的数据完成下列![]() 列联表,问:能否有
列联表,问:能否有![]() 的把握认为“移动支付活跃用户”与性别有关?
的把握认为“移动支付活跃用户”与性别有关?
非移动支付活跃用户 | 移动支付活跃用户 | 总计 | |
男 | |||
女 | |||
总计 |
附参照表:
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: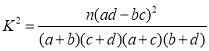 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有400名学生参加某项体育测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图:
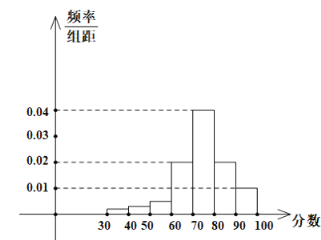
(1)若该样本中男生有55人,试估计该学校高三年级女生总人数;
(2)若规定小于60分为“不及格”,从该学校高三年级学生中随机抽取一人,估计该学生不及格的概率;
(3)若规定分数在![]() 为“良好”,
为“良好”,![]() 为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次会操活动中,领操员让编号为![]() 的
的![]() 名学生排成一个圆形阵,做
名学生排成一个圆形阵,做![]() 循环报数,领操员一一记录报数者的编号,并要求报l、2的学生出列,报3的学生留在队列中,并将编号改为此次循环报数中三名学生的编号之和.一直循环报数下去.当操场上剩余的学生人数不超过两名时,报数活动结束.领操员记录最后留在操场的学生编号(例如,编号为
循环报数,领操员一一记录报数者的编号,并要求报l、2的学生出列,报3的学生留在队列中,并将编号改为此次循环报数中三名学生的编号之和.一直循环报数下去.当操场上剩余的学生人数不超过两名时,报数活动结束.领操员记录最后留在操场的学生编号(例如,编号为![]() 的九名学生排成一个圆形阵,报数结束后,只有原始编号为9的学生留在操场,此时,他的编号为45,领操员记录下来的数据分别为l,2,3,4,5,6,7,8,9,6,15,24,45).已知共有2011名学生参加会操.
的九名学生排成一个圆形阵,报数结束后,只有原始编号为9的学生留在操场,此时,他的编号为45,领操员记录下来的数据分别为l,2,3,4,5,6,7,8,9,6,15,24,45).已知共有2011名学生参加会操.
(1)最后留在场内的学生最初的编号是几号?
(2)求领操员记录下的编号之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在股票市场上,投资者常根据股价![]() 每股的价格
每股的价格![]() 走势图来操作,股民老张在研究某只股票时,发现其在平面直角坐标系内的走势图有如下特点:每日股价
走势图来操作,股民老张在研究某只股票时,发现其在平面直角坐标系内的走势图有如下特点:每日股价![]() 元
元![]() 与时间
与时间![]() 天
天![]() 的关系在ABC段可近似地用函数
的关系在ABC段可近似地用函数![]() 的图象从最高点A到最低点C的一段来描述
的图象从最高点A到最低点C的一段来描述![]() 如图
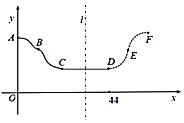
如图![]() ,并且从C点到今天的D点在底部横盘整理,今天也出现了明显的底部结束信号.老张预测这只股票未来一段时间的走势图会如图中虚线DEF段所示,且DEF段与ABC段关于直线l:
,并且从C点到今天的D点在底部横盘整理,今天也出现了明显的底部结束信号.老张预测这只股票未来一段时间的走势图会如图中虚线DEF段所示,且DEF段与ABC段关于直线l:![]() 对称,点B,D的坐标分别是
对称,点B,D的坐标分别是![]() .
.
![]() 请你帮老张确定a,
请你帮老张确定a,![]() ,
,![]() 的值,并写出ABC段的函数解析式;
的值,并写出ABC段的函数解析式;
![]() 如果老张预测准确,且今天买入该只股票,那么买入多少天后股价至少是买入价的两倍?
如果老张预测准确,且今天买入该只股票,那么买入多少天后股价至少是买入价的两倍?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述正确的是( )
A.相关关系是一种确定性关系,一般可分为正相关和负相关
B.回归直线一定过样本点的中心![]()
C.在回归分析中,![]() 为0.98的模型比
为0.98的模型比![]() 为0.80的模型拟合的效果好
为0.80的模型拟合的效果好
D.某同学研究卖出的热饮杯数![]() 与气温
与气温![]() 的关系,得到回归方程
的关系,得到回归方程![]() ,则气温为2℃时,一定可卖出142杯热饮
,则气温为2℃时,一定可卖出142杯热饮
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月份,我国湖北武汉出现了新型冠状病毒,人感染后会出现发热、咳嗽、气促和呼吸困难等,严重的可导致肺炎甚至危及生命.为了增强居民防护意识,增加居民防护知识,某居委会利用网络举办社区线上预防新冠肺炎知识答题比赛,所有居民都参与了防护知识网上答卷,最终甲、乙两人得分最高进入决赛,该社区设计了一个决赛方案:①甲、乙两人各自从![]() 个问题中随机抽
个问题中随机抽![]() 个.已知这
个.已知这![]() 个问题中,甲能正确回答其中的
个问题中,甲能正确回答其中的![]() 个,而乙能正确回答每个问题的概率均为
个,而乙能正确回答每个问题的概率均为![]() ,甲、乙两人对每个问题的回答相互独立、互不影响;②答对题目个数多的人获胜,若两人答对题目数相同,则由乙再从剩下的
,甲、乙两人对每个问题的回答相互独立、互不影响;②答对题目个数多的人获胜,若两人答对题目数相同,则由乙再从剩下的![]() 道题中选一道作答,答对则判乙胜,答错则判甲胜.
道题中选一道作答,答对则判乙胜,答错则判甲胜.
(1)求甲、乙两人共答对![]() 个问题的概率;
个问题的概率;
(2)试判断甲、乙谁更有可能获胜?并说明理由;
(3)求乙答对题目数的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() 使得直线
使得直线![]() 与直线
与直线![]() 恰关于
恰关于![]() 轴对称?若存在,求出点
轴对称?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com