Question

9．给出以下命题：
（1）函数f（x）=$\sqrt{{x}^{2}}$与函数g（x）=|x|是同一个函数；
（2）函数f（x）=a^x+1（a＞0且a≠1）的图象恒过定点（0，1）；
（3）设指数函数f（x）的图象如图所示，若关于x的方程f（x）=$\frac{m-1}{m+1}$有负数根，则实数m的取值范围是（1，+∞）；
（4）若f（x）=$\left\{\begin{array}{l}{{2}^{x}+t（x≥0）}\\{g（x）（x＜0）}\end{array}\right.$为奇函数，则f（f（-2））=-7；
（5）设集合M={m|函数f（x）=x²-mx+2m的零点为整数，m∈R}，则M的所有元素之和为15．
其中所有正确命题的序号为（　　）

• A． （1）（2）（3）
• B． （1）（3）（5）
• C． （2）（4）（5）
• D． （1）（3）（4）

Answer 1

分析 （1）根据同一函数的定义和性质进行判断．
（2）根据指数函数过定点的性质进行判断．
（3）根据指数函数的图象和性质先求出函数的解析式，结合指数函数的取值范围进行求解即可．
（4）根据函数奇偶性的性质，利用转化法进行求解．
（5）根据根与系数之间的关系进行判断即可．

解答 解：（1）函数f（x）=$\sqrt{{x}^{2}}$=|x|，函数g（x）=|x|，则两个函数是同一个函数；正确．
（2）∵f（0）=a⁰+1=1+1=2，∴函数f（x）=a^x+1（a＞0且a≠1）的图象恒过定点（0，2）；故（2）错误，
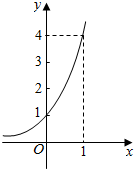
（3）设指数函数f（x）的图象如图所示，
则设f（x）=a^x，由f（1）=4得a=4，即f（x）=4^x，
若关于x的方程f（x）=$\frac{m-1}{m+1}$有负数根，
则当x＜0时，0＜f（x）＜1，
由0＜$\frac{m-1}{m+1}$＜1，即$\left\{\begin{array}{l}{\frac{m-1}{m+1}＞0}\\{\frac{m-1}{m+1}＜1}\end{array}\right.$，即$\left\{\begin{array}{l}{m＞1或m＜-1}\\{\frac{m-1}{m+1}-1=\frac{-2}{m+1}＜0}\end{array}\right.$，
得$\left\{\begin{array}{l}{m＞1或m＜-1}\\{m＞-1}\end{array}\right.$，
即m＞1，
则实数m的取值范围（1，+∞）；故（3）正确，
（4）若f（x）=$\left\{\begin{array}{l}{{2}^{x}+t（x≥0）}\\{g（x）（x＜0）}\end{array}\right.$为奇函数，
则f（0）=0，即1+t=0，即t=-1，即当x≥0时，f（x）=2^x-1．
则f（-2）=-f（2）=-（2²-1）=-3，
则f（f（-2））=f（-3）=-f（3）=-（2³-1）=-7；故（4）正确，
（5）∵函数f（x）=x²-mx+2m的零点为整数，
∴判别式△=m²-8m≥0，解得m≥8或m≤0，
x₁+x₂=m，x₁x₂=2m，
则x₁x₂=2（x₁+x₂），
即（x₁-2）（x₂-2）=4，
不妨设x₁≤x₂，由整数的性质得
①x₁-2=2且x₂-2=2，此时x₁=4，x₂=4，此时m=4+4=8，
②x₁-2=1且x₂-2=4，此时x₁=3，x₂=6，此时m=3+6=9，
③x₁-2=-2且x₂-2=-2，此时x₁=0，x₂=0，此时m=0+0=0，
④x₁-2=-4且x₂-2=-1，此时x₁=-2，x₂=1，此时m=-2+1=-1，
从而得到M={8，9，-1，0}，所有元素之和为16，故（5）错误．
故所有正确命题的序号为（1）（3）（4）．
故答案为：（1）（3）（4）．

点评 本题主要考查与函数有关的命题的真假判断，涉及指数函数，函数的零点和概念，综合性较强，利用定义法和转化法是解决本题的关键．