
【题目】求证: ![]() ﹣
﹣ ![]() <
< ![]() ﹣
﹣ ![]() (a≥3).
(a≥3).
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:高中数学 来源: 题型:
【题目】设连续掷两次骰子得到的点数分别为m、n,令平面向量 ![]() ,
, ![]() .
.
(1)求使得事件“ ![]() ”发生的概率;
”发生的概率;
(2)求使得事件“ ![]() ”发生的概率;
”发生的概率;
(3)使得事件“直线 ![]() 与圆(x﹣3)2+y2=1相交”发生的概率.
与圆(x﹣3)2+y2=1相交”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() 是定义在(﹣1,1)上的奇函数,且
是定义在(﹣1,1)上的奇函数,且 ![]() .
.
(1)确定函数的解析式;
(2)证明函数f(x)在(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若实数![]() 满足
满足![]() ,则称
,则称![]() 为函数
为函数![]() 的不动点.
的不动点.
(1)求函数![]() 的不动点;
的不动点;
(2)设函数![]() ,其中
,其中![]() 为实数.
为实数.
① 若![]() 时,存在一个实数
时,存在一个实数![]() ,使得
,使得![]() 既是
既是![]() 的不动点,又是
的不动点,又是![]() 的不动点(
的不动点(![]() 是函数
是函数![]() 的导函数),求实数
的导函数),求实数![]() 的取值范围;
的取值范围;
② 令![]() ,若存在实数
,若存在实数![]() ,使
,使![]() ,
,![]() ,
,![]() ,
,![]() 成各项都为正数的等比数列,求证:函数
成各项都为正数的等比数列,求证:函数![]() 存在不动点.
存在不动点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
(1)根据上表数据,请在如图坐标系中画出散点图; 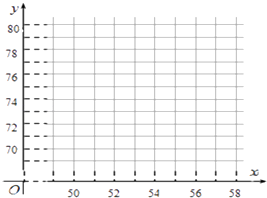
(2)根据上表数据,用最小二乘法求出y关于x的线性回归方程 ![]() ;(保留2位小数)
;(保留2位小数)
(3)若周六同一时间段车流量是25万辆,试根据(2)求出的线性回归方程预测,此时PM2.5的浓度为多少(保留整数)?
参考公式: ![]() =
= 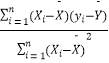 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x3+ax2+1,(a∈R).
(1)若f(x)图象上横坐标为1的点处存在垂直于y轴的切线,求a的值;
(2)若f(x)在区间(﹣1,2)内有两个不同的极值点,求a取值范围;
(3)当a=1时,是否存在实数m,使得函数g(x)=x4﹣5x3+(2﹣m)x2+1的图象于函数f(x)的图象恰有三个不同的交点,若存在,试求出实数m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F(0,1),直线l:y=﹣1,P为平面上的动点,过点P作直线l的垂线,垂足为Q,且 ![]() .
.
(1)求动点P的轨迹C的方程;
(2)已知圆M过定点D(0,2),圆心M在轨迹C上运动,且圆M与x轴交于A、B两点,设|DA|=l1 , |DB|=l2 , 求 ![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com