
�������ѧ��쳲�����(L��Fibonacci)������1228���ġ��㾭��һ���м�������Ȥ���������⣺�ٶ�ÿ�Դ�����ÿ������һ��С���ӣ���ÿ��С���ӹ���һ���¾Ϳɳ��ɴ����ӣ������������������ô��һ�Դ����ӿ�ʼ��һ������ж��ٶԴ������أ�
�������θ��������µĴ����Ӷ�������һֱ������ȥ�������������ɵ����У�
1��1��2��3��5��8��13��21��34��55��89��144��233������
�����쳲��������У���������a1��a2��1�����ܹ��ɳ���n��3ʱan�ĵ��ƹ�ϵʽ��
 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015���Ĵ��ɶ�����ʵ��ѧУ��һ3���¿���ѧ�Ծ��������棩 ���ͣ�ѡ����
1202�꣬�������ѧ��쳲��������������и�����һ���������ӷ�ֳ�ĵ��ƹ�ϵ�� ��
�� ��������
�������� ��ʾ��
��ʾ�� ���µ����ӵ��ܶ�����
���µ����ӵ��ܶ����� ����
����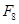 ��ֵΪ�� ��
��ֵΪ�� ��
A��13 B��21 C��34 D��55
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012-2013ѧ��㶫ʡ��ɽ�и߶����ϣ���ĩ��ѧ�Ծ����Ŀƣ��������棩 ���ͣ�ѡ����
 �ɴ˿ɼ����F7=�� ��
�ɴ˿ɼ����F7=�� ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com